top of page

検索


双対行列を用いたエントロピー増大則の説明(1)~2*2行列の場合までの考察~
[1] https://jp.dreamscope.me/blog/2021/4/entropy 「エントロピー増大の法則とは?」 [2] 「工業熱力学」第2版 [3] 「弾性力学の基礎」 [4] https://isiotoyume.wixsite.com/website...
S Y
2022年8月27日読了時間: 4分


(ε_k+(t^)ε_k)^mおよび(ε_k-(t^)ε_k)^mの計算結果一覧
k=2 k=3 k=4 ここでa_kは、a_0=0, a_1=1とした場合の、フィボナッチ数列です。 4n+1=mとしてます。 (訂正) 4n+4乗の4*4はa_m+2ではなく、a_(m+2)。以下を参照のこと k=5 k=6以降については、かなり不規則な値を取ります。...
S Y
2022年8月24日読了時間: 1分


足し算的な性質により、素数表を作成してみた
0.参考文献 [1]https://isiotoyume.wixsite.com/website/post/フィボナッチ数列の性質一覧-備忘録 1.Nボナッチ数列についての一般化されたゼッケンドルフ=石音の定理について 復習です。Nボナッチ数列は、(N-2)個まで隣り合う数...
S Y
2022年8月13日読了時間: 2分


双対数を行列化してみたら、ハイゼンベルクの不確定性原理っぽいのができた話
0.参考文献 [1]https://manabitimes.jp/math/1307 [2]https://ja.wikipedia.org/wiki/不確定性原理 [3]https://7shi.hateblo.jp/entry/2019/11/24/044617...
S Y
2022年8月12日読了時間: 2分


ヴァンティーンゲムの結果はウィルソンの定理と同値であろうか?
0.参考文献 [1] 「数論<未解決問題>の事典」 リチャード・K・ガイ著 金光滋訳 朝倉書店 2010年11月5日初版出版 p.55 1.ヴァンティーンゲムの結果とウィルソンの定理 ヴァンティーンゲムの結果は以下の通りです。...
S Y
2022年8月9日読了時間: 2分


*e^(ε*)という作用素に対する考察
1.作用素の定義 このような変換が成立する関数f(x)は、おそらく定まる(任意ではない)。これはどのような関数でしょうか? 2.解 まず、ネイピア数を消去します。 ここに、x=y+εを代入します。 2.1 k=1の時 以上から、f(y)=g(y)→f'(y)=g'(y)とな...
S Y
2022年8月7日読了時間: 1分
![ラプラス変換・逆ラプラス変換を用いた任意の関数における微小空間[εs]での零点存在証明および、ある1つの例外を除いた特異点存在証明](https://static.wixstatic.com/media/e2c195_ee03d22ca14944a59f071a55a916f2ab~mv2.png/v1/fill/w_358,h_101,fp_0.50_0.50,lg_1,q_35,blur_30,enc_avif,quality_auto/e2c195_ee03d22ca14944a59f071a55a916f2ab~mv2.webp)
![ラプラス変換・逆ラプラス変換を用いた任意の関数における微小空間[εs]での零点存在証明および、ある1つの例外を除いた特異点存在証明](https://static.wixstatic.com/media/e2c195_ee03d22ca14944a59f071a55a916f2ab~mv2.png/v1/fill/w_256,h_72,fp_0.50_0.50,q_95,enc_avif,quality_auto/e2c195_ee03d22ca14944a59f071a55a916f2ab~mv2.webp)
ラプラス変換・逆ラプラス変換を用いた任意の関数における微小空間[εs]での零点存在証明および、ある1つの例外を除いた特異点存在証明
よって、仮定が成り立つ関数に [1] 理工系の数学入門コース[新装版] フーリエ解析 大石進一 岩波書店 1.ラプラス変換と逆ラプラス変換 ラプラス変換は次のように与えられます。 ラプラス逆変換は次のように与えられます。...
Yume Isioto
2022年7月31日読了時間: 2分


四次元ポケットの理論設計(その2) ~ランベルトのW関数とホーキング放射~
0.参考文献 [1]https://isiotoyume.wixsite.com/website/post/四次元ポケットの理論設計 [2]https://ja.wikipedia.org/wiki/ランベルトのW関数 [3]https://ja.wikipedia.org...
S Y
2022年7月19日読了時間: 4分


1:2:sqrt(5)に近似的に相似なピタゴラス数による直角三角形の描画方法に関する考察及び、フェルマーの最終定理についての考察
0.参考文献 [1]https://manabitimes.jp/math/661 ピタゴラス数の求め方とその証明(特に、原始ピタゴラス数の求め方が記されている) 1.原始ピタゴラス数[1] ピタゴラス数はある意味で無限に存在します。例えば、一つのピタゴラス数を見つけた場合...
S Y
2022年7月19日読了時間: 2分


微小複素領域εsにおけるζ関数の零点はどこにあるか?
0.参考文献 [1]https://ja.wikipedia.org/wiki/リーマンゼータ関数 1.微小複素領域におけるζ関数の表示方法 初めに、複素領域におけるゼータ関数を示します。 sの代わりにεsを代入すると、次のようになります。同時に、Γ関数も変化します。...
S Y
2022年7月12日読了時間: 3分


異なる2つの二項演算を"直交"させたときに現れる新たな"数"の性質に関する、係数を用いた調査
0.定義 次のルールで表を埋めていきます。 異なる数x,yを考えます。あるマスにxが、その左隣にyがあるとします。これを数とみなし、左右方向に次元の低い演算(例えば足し算)を行います。右側を正として加法、左側を負として減法とします。上下方向に次元の高い演算(例えば掛け算)を...
S Y
2022年7月12日読了時間: 2分


ABC予想とトーシェント関数の関係
0.参考文献 [1]https://ja.wikipedia.org/wiki/ABC予想 [2]https://ja.wikipedia.org/wiki/オイラーのφ関数 1.トーシェント関数 自然数に対して、一意に素因数分解を与えることができます。...
S Y
2022年7月12日読了時間: 1分


2の冪乗数列とゼータ関数の関係
0.参考文献 [1]https://isiotoyume.wixsite.com/website/post/nボナッチ数列及び2の冪乗数列に関する三角関数を用いた漸化式 [2] https://isiotoyume.wixsite.com/website/post/フィボナ...
S Y
2022年7月5日読了時間: 1分

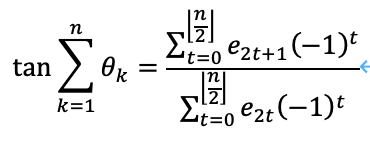
Nボナッチ数列及び2の冪乗数列に関する三角関数を用いた漸化式
0.参考文献 [1] https://manabitimes.jp/math/1277 タンジェントの加法定理とその拡張 1.tangentの加法定理 ここでe_iはtanθ_1~tanθ_nのi次の基本対称式です。e_0=1、i>n→e_i=0。基本対称式は、「n個のもの...
S Y
2022年7月4日読了時間: 1分


トリボナッチ数列の三角関数を用いた漸化式
0.参考文献 [1]https://manabitimes.jp/math/578 tangentの美しい関係式 高校数学の美しい物語 1.tangentの美しい関係式[1] 参考文献[1]によれば、以下の関係式が成り立ちます。...
S Y
2022年7月4日読了時間: 1分


フィン効率を100%にするための長さの設計値を求めよ、ただし複素数解で良いとし、0ではないとする。
0.参考文献 [1]https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwiSk5Og5tL4AhViUfUHHXmaBaQQFnoECEcQAQ&url=http%3A%2F%2...
S Y
2022年6月30日読了時間: 1分


y=cosh(axcos(bxy))の停留点を求める
[1]https://isiotoyume.wixsite.com/website/post/乱流解析に関する予想-テニスラケットの原理を使用 [2]https://isiotoyume.wixsite.com/website/post/γtan-γ-1を満たす数に対する考...
S Y
2022年6月23日読了時間: 2分


フィボナッチ数と奇素数の級数を用いた関係式(ゼータ関数と関係あり)
[1]https://isiotoyume.wixsite.com/website/post/フィボナッチ数列の三角関数-tangent-を用いた漸化式 [2]https://manabitimes.jp/math/1381...
S Y
2022年6月20日読了時間: 2分


γtan(γ)=1を満たす数に対する考察
0.参考文献 なし 1.以下の問いに答えよ γtan(γ)=1を満たす数を、整数kを用いて表せ。 2.解法 次のように連立方程式として解くことにします。 余談ですが、γ_2はオイラー座屈で見たことがある式ですね。 両辺をかけて整理することで次の結果を得ます。 追記(6/20...
S Y
2022年6月19日読了時間: 2分


フィボナッチ数を用いて、宇宙の形を調べる〜曲率の話〜
0. 参考文献 [1]https://www.ms.u-tokyo.ac.jp/~kohno/lectures/FridayHS.pdf [2]https://isiotoyume.wixsite.com/website/post/三角形の3辺がフィボナッチ数であるような三...
S Y
2022年6月15日読了時間: 2分
bottom of page