*e^(ε*)という作用素に対する考察

1.作用素の定義

このような変換が成立する関数f(x)は、おそらく定まる(任意ではない)。これはどのような関数でしょうか？

2.解

まず、ネイピア数を消去します。

ここに、x=y+εを代入します。

2.1 k=1の時

以上から、f(y)=g(y)→f'(y)=g'(y)となり、結局

となります。

すなわち、任意の複素数sを用いて、f(y)=sεであることがわかります。

2.2 一般の時

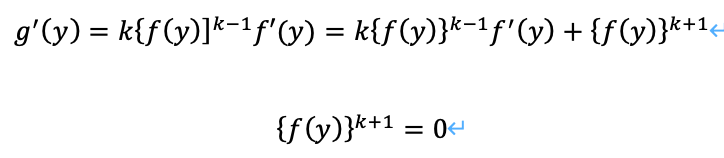
すると、次のように変換することができます。(sを任意の複素数とします)

3.まとめ

ラプラス変換を参考に、ネイピア数の双対数乗を考えました。こうすれば、任意の関数に対して、新たな変換が可能であると考えましたが、結局単に双対数による関数における、隣り合う自然数の商での乗算であることがわかりました。