Nボナッチ数列及び2の冪乗数列に関する三角関数を用いた漸化式

0.参考文献

[1] https://manabitimes.jp/math/1277

タンジェントの加法定理とその拡張

1.tangentの加法定理

ここでe_iはtanθ_1~tanθ_nのi次の基本対称式です。e_0=1、i>n→e_i=0。基本対称式は、「n個のものからi個選んで掛け合わせ、全通りについて足したもの」です。

2.N=2の時

以下のようになります。また、フィボナッチ数を用いて考えることができます。

以上から、以下の2つの漸化式が成立します。

3.N=3の時

以下のようになります。また、トリボナッチ数を用いて考えることができます。

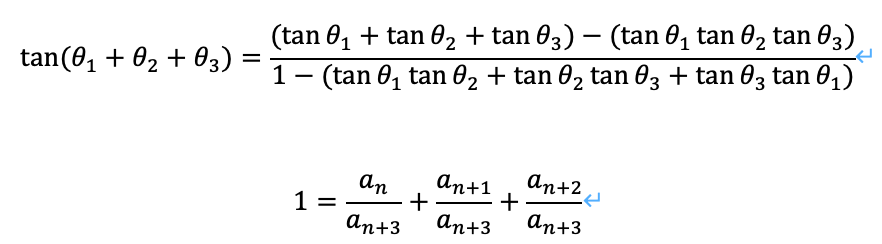
以上から、次の2つの漸化式が成立します。

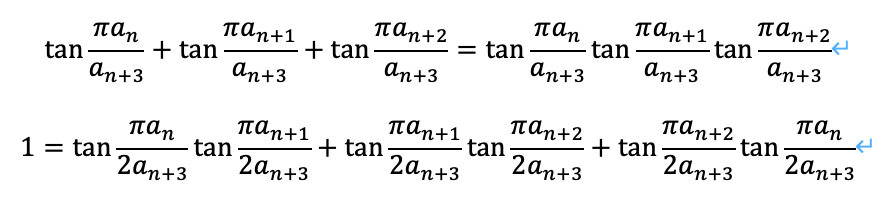
前回の記事の通り、特にsinを使って考えることができます。新たに導いた下段の漸化式に対しても同様にsinとcosを用いて表すことができるでしょう。

4.N→∞の時

そもそも、N→∞とはどういう数列でしょうか？結論、2の冪乗数列となります。初項を1とすれば、前までの項をいつでも全部足すことになるので、

1,1,2,4,8,16,32,64,128,...

となるためです。

以上から、同様に考えていくと、結局次の公式を与えることができます。

煩雑でわかりにくいので、以下のように書き換えます。

計算方法上、mの範囲指定(∏)とl_m(Σ)の表記が逆になることに注意してください。