ラプラス変換・逆ラプラス変換を用いた任意の関数における微小空間[εs]での零点存在証明および、ある1つの例外を除いた特異点存在証明

よって、仮定が成り立つ関数に

[1] 理工系の数学入門コース[新装版]　フーリエ解析　大石進一　岩波書店

1.ラプラス変換と逆ラプラス変換

ラプラス変換は次のように与えられます。

ラプラス逆変換は次のように与えられます。

これは結局、複素数s=a+ibに対して、bについてフーリエ変換を行うことを考えているのと同値です。これにより、実数関数を複素数関数とすることができます。

2.双対数を用いたラプラス変換

公式を用いることにより、次のようにかけます。

これは、後で用います。

3.双対数を用いた逆ラプラス変換

(修正 8/1)　虚部について、i/ε→i/ε^3とするのが正しいです。

逆ラプラス変換では、2πiがかかるため、簡単のために変形しました。

ただし、-n階微分はn階積分と同値です。

簡単に整理させるため、以下の変数に置き換えます。

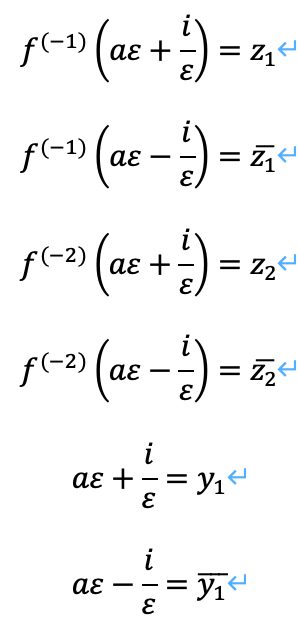
4.2章と3章の合わせ技

逆ラプラス変換をした後に、ラプラス変換をします。

ここに、0=ε^2、∞=1/ε^2であることを用いて展開すれば、次のようになります。

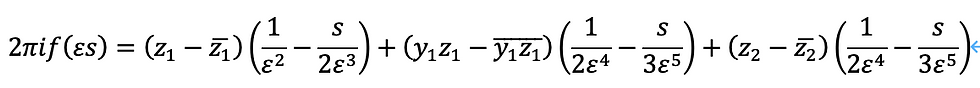
さて、ここにf(εs)=0を満たす零点が存在するとすれば、これを満たすsは幾つでしょうか？左辺を0として、右辺をsについて解けば次のようになります。

4.1 仮定1

以下の式を仮定します。

この時、4章の式からs=2εであることがわかります。

4.2 仮定2

以下の式を仮定します。

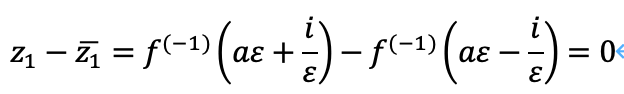
これは結局、関数f(εs)=0であるか、虚部について奇関数であることがわかります。

この時、s=3/2εであることがわかります。

4.3 仮定1かつ仮定2

この時、s=3εとなることがわかります。

共通する修正

(修正 8/1)　虚部について、i/ε→i/ε^3とするのが正しいです。