(ε_k+(t^)ε_k)^mおよび(ε_k-(t^)ε_k)^mの計算結果一覧

k=2

k=3

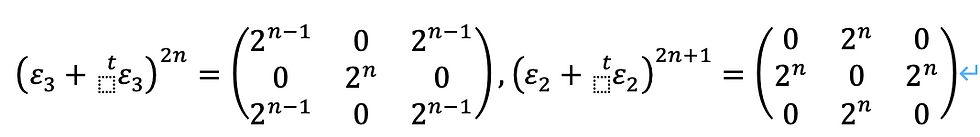
k=4

ここでa_kは、a_0=0, a_1=1とした場合の、フィボナッチ数列です。

4n+1=mとしてます。

(訂正) 4n+4乗の4*4はa_m+2ではなく、a_(m+2)。以下を参照のこと

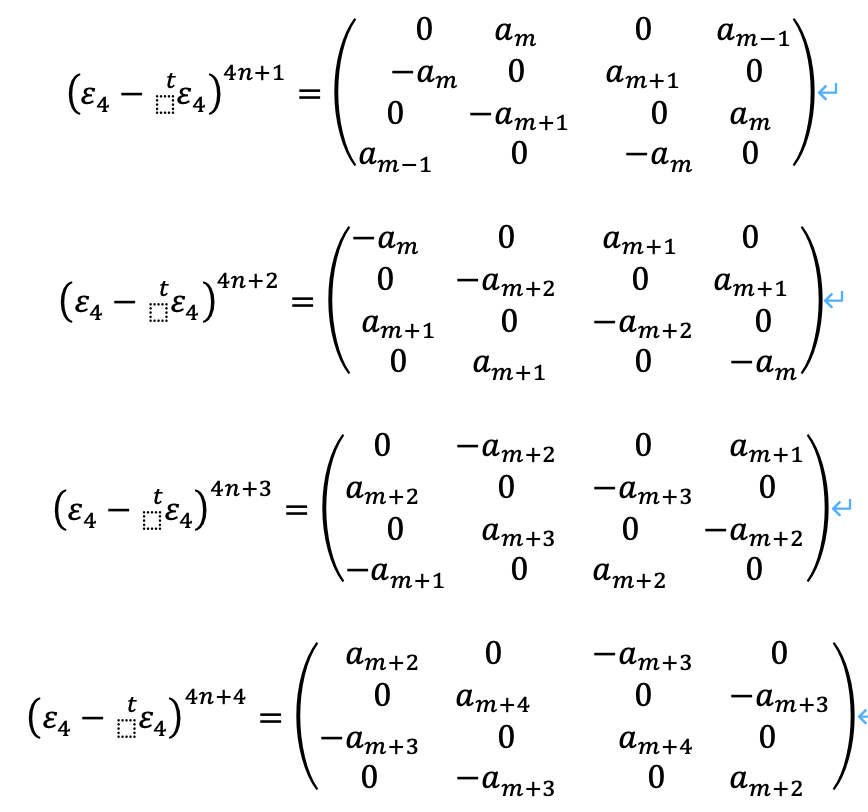
k=5

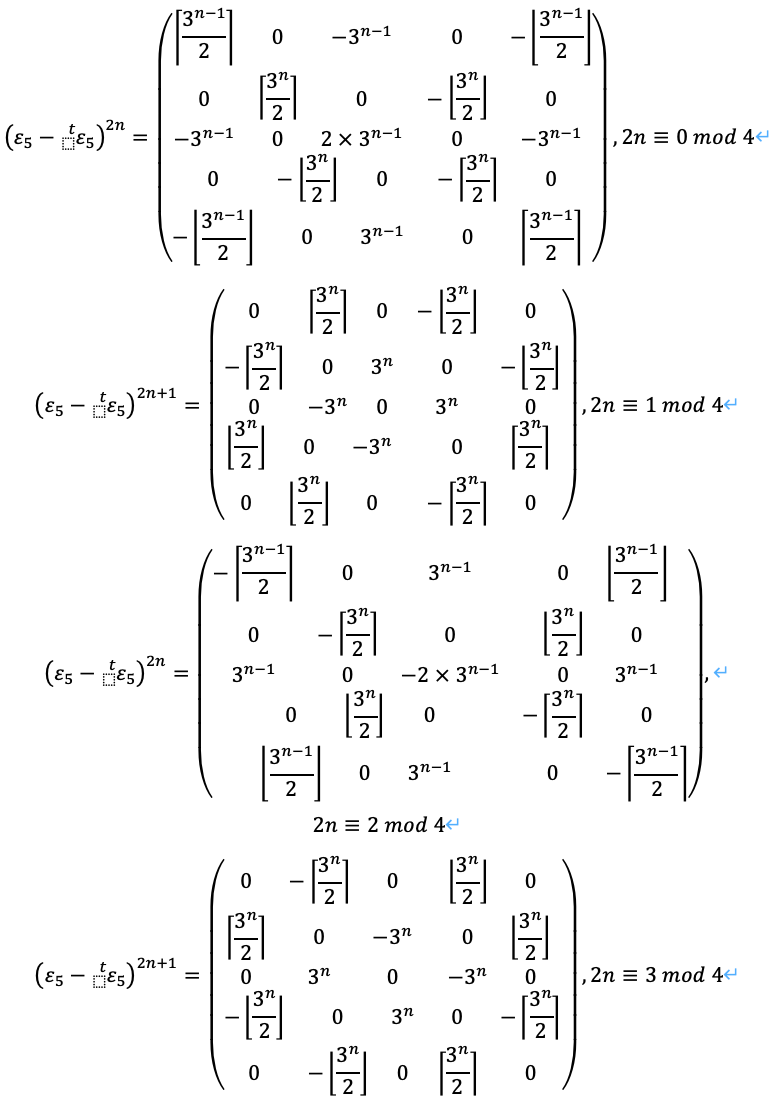
k=6以降については、かなり不規則な値を取ります。

n=1

n=2

n=3

n=4

n=5

n=6

n=7

n=8

n=9

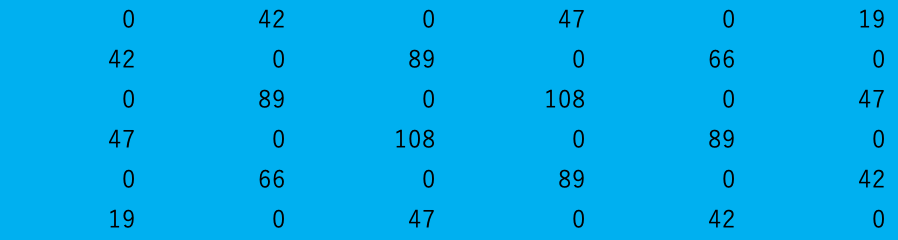
n=10

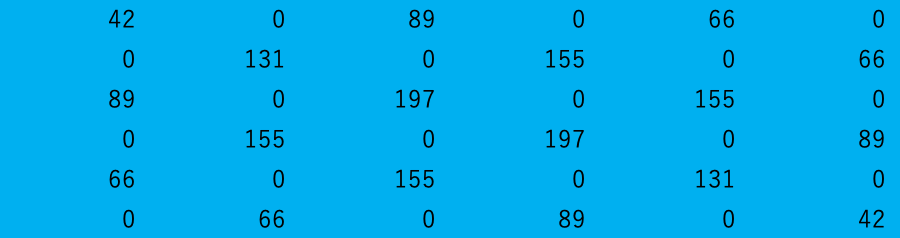
ただし、定義から明らかなように0を挟んだ上下左右において、

上+下=右+左

の関係が必ず成り立ちます。(仮に行列において0の隣が端の行または列であったとしても、本来数のあるところに0を仮定することで成立します。)

131=42+89, 89+197=131+155, etc...

このことから、加法を用いることにより容易に次に次数の大きい行列を計算でき、反対に減法を用いることである行列から次数を低くすることもできます。

ところが、行列演算という視点で考えると、残念ながらε_k+(t^)ε_kの逆行列が存在しないために、"除法"はできないことがわかります。

この性質について、次の記事で詳しく考察します。

ちなみにスクリーンショットでお察しの通り、これはExcelのMMULT関数を用いることにより容易に計算することができます。