双対行列を用いたエントロピー増大則の説明(1)~2*2行列の場合までの考察~
- S Y
- 2022年8月27日
- 読了時間: 4分
[1] https://jp.dreamscope.me/blog/2021/4/entropy 「エントロピー増大の法則とは?」
[2] 「工業熱力学」第2版
[3] 「弾性力学の基礎」
1.エントロピー増大則とは?[1][2][5]
断熱系において、そのエントロピーは時間発展すれば増大する法則のことです。
ギブスの式
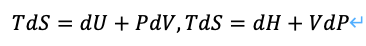
からわかるように、仕事と内部エネルギーをそれぞれ変化させることにより摩擦が生じ、これがエントロピーとなる(無効エネルギーが生ずる)ことがわかります。
摩擦のないように時間変化させることは不可能ですから、エントロピーは当然、増大します。
比熱を用いることで、有名な以下の式が得られます。

ところで、ボルツマンによれば、エントロピーを次のように定義することができるそうです。
W: 全部の状態数

実際、エントロピーの変化を、状態数の変化がT_1→T_2、定数k=mcを用いることにより先ほどの式となることがわかります。
2.応力テンソルと主応力 [3]
ある直方体を考えます。ここに3軸(x,y,z)を与え、各軸に並行な面に加わる軸力及び剪断力について、以下のような応力テンソルを考えます。

この行列を固有値及び固有ベクトルにより対角化することで、主応力を求めることができます。
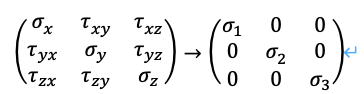
対角化することで計算が容易になりました。
3. (ε_n+(t^)ε_n)^mについて [4]
前回の記事にて、いつでも上+下=右+左が成り立つような、逆行列を持たない行列について考察しました。
この行列の特徴として
1 逆行列を持たないこと
2 行列の各要素は加法により漸化式が存在し、値は増加すること
3 0の位置は奇数乗と偶数乗により入れ替わり(振動し)、0を中心に上+下=右+左が成立する
が挙げられることを確認しました。
この特徴が、エントロピーの特徴と類似していることに気づきます。
1 エントロピーの方向の存在(不可逆性)
2 「時間の矢」の過去、現在、及び未来への発展性(エントロピーの増加)
3 「エントロピーの流量」なるものが行列の要素とみなした時、流れの方向は互いに打ち消しあい、見かけ上釣り合う
(ただし、左右方向については方向が一意には定まらないので、揺れ動く。これが見かけ上、0の位置が奇数か偶数かで分かれる要因であると捉える)
以上から、エントロピーの特徴と双対空間が類似していることがわかりますから、正しいと仮定しましょう。
温度Tはボルツマン定数kを用いて運動エネルギーK(分子運動。格子の振動を含む)に変換できますので、本質的には分子運動と温度はボルツマン定数kを通じて相似関係にあることがわかります。
3.1 2*2行列の場合のエントロピーと温度
エントロピーが双対空間で表せるとすれば、以下のように仮定できます。
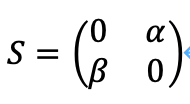
この時、次のように表せます。

エントロピーを元に、温度がどうなるのかを考えます。
方法は以下の通りです。
1) 行列Sを対角化する
2) 対角化した行列Σに対して、exp(Σ)を考える
3) exp(Σ)を用いて、exp(S)を算出
4) ボルツマン定数の逆数1/kについて、(1/k)E(Eは単位行列)をかけることにより、温度行列Tを算出する
まずは、対角化します。
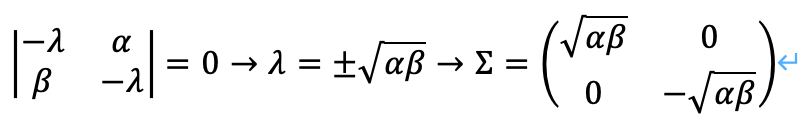
対角化した場合、このn乗を考えると、a_(m*m)の成分について、a_(m*m)^nとなり、他はそのまま0となることがわかります。
その結果、任意の行列Aに対してもexp(A)を容易に求めることができるようになります。

正規化した固有ベクトルを考えます。

よって、固有ベクトルは次のとおりです。

以上から、次のように計算できます。

ここに、ボルツマン定数kを導入することにより、温度ベクトルは次のとおりとなることがわかります。

3.2 温度ベクトルの大きさ
温度ベクトルの大きさは、計算することで1/(k(α+β))であることがわかります。
3.3 テニスラケットの原理を用いた乱流解析についての考察[5]
以前の記事にて、乱流の主要因がテニスラケットの原理であるとした場合の、分子の三軸角速度を求めました。以下の通りです。

運動エネルギーについて、以下の関係にあります。

これをTについて整理します。ここに、A^2=3/(I_x)、B^2=3/(I_y+I_z)とします。

ところでTと示しましたが、Tはここではスカラー量ですから、|T|=1/(k(α+β))となります。
すると、以下の補題を考えた後、議論すべきであることが推測できます。
(補題)

とした時、aとbをそれぞれc,dを用いて表せ。
解)
うまいこと、三角関数を用いてパラメータ表示しましょう。

と置きます。そして、a+b=(p+iq)(p-iq)を用いて次のように変形できることに気づきます。

ここまでくると、ピタゴラスの定理、sinθ^2+cosθ^2=1に気づきます。
見方の違い(90度回転)でどちらを正弦に、どちらを余弦にするかが変わりますが、今回は以下のように置きます。
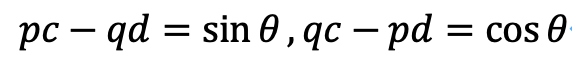
この結果から、pとqについての連立方程式になることがわかりますので、これを解いて、次の結果を得ます。

以上から、aとbについて以下の結果を得ます。

(補題の解答終わり)
kTについての式において、以下のようにc,dを置くことでT=1/(α+β)を考えることができます。

以上から、

であることがわかります。
以下のようにCとDを定めます。

以上から、温度Tについて次のように行列で表せます。

また、この結果をもとに、エントロピーSについても行列で表せることがわかります。
ここに、mは0または1です。



コメント