フィボナッチ数と奇素数の級数を用いた関係式(ゼータ関数と関係あり)

[1]https://isiotoyume.wixsite.com/website/post/フィボナッチ数列の三角関数-tangent-を用いた漸化式

1.tangentのテイラー展開[2][3]

tangentのテイラー展開は次のようになることが知られています。

ここで、B_(2s)は2s番目のベルヌーイ数です。

さらに、ベルヌーイ数についてゼータ関数の関係から、次のように与えられます。

そのため、ゼータ関数を用いたtangentの表記は次のようになります。

(7/5追記)　π^(2n)となってましたが、π^(2s)の誤りです。

2.フィボナッチ数列のtangentを用いた漸化式[1]

以前の記事で証明したように、次の漸化式が成り立ちます。

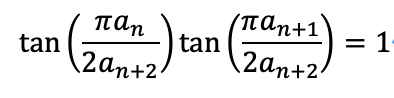
3.arctangentの無限級数表現

arctangentのテイラー展開は以下のようになることが知られています。

特にarctan(1)=π/4は、πの近似を与える上でよく使われます。

4.フィボナッチ数と奇素数の級数を用いた関係式

ゼータ関数を用いたtangetの表記より、級数の形について整理すれば、最終的に以下のようになります。

追記(6/20 16:29) 4^n-1と4^(n-1)はそれぞれnが誤りで、正しい文字はsです。

4^s-1や、4^(s-1)を消去すべく、ゼータ関数においてpの範囲から2を除きます。すなわち、奇素数についての無限積に変換します。また、二つの無限級数項について、それぞれの相乗平均を考えると、次のようになります。

(右辺を1にするために、π/4で両辺を割ります。)

両辺のarctangentについて考え、テイラー展開を用いることにより以下の関係式を得ます。

よって、任意に選択した(有限とは限らない、空集合ではないような)自然数の部分集合N'において以下の関係にあります。

こうして、奇数、奇素数、フィボナッチ数、円周率の関係式を得ることができました。

(6/20 23:05追記　4/πの項の抜けを修正)

→自然数集合による無限積は本当は一番左

あるいは、次のようにかけます。

nを十分に大きく取り、かつN'の要素数を1とすれば黄金比φを用いることで次の結果を得ます。

最新記事