素数のなす空間が、フィボナッチ数のなす空間とは異なる話(素数の空間は、ダブルトーラスか?)
- S Y
- 2022年12月20日
- 読了時間: 4分
0.参考文献
[1]
[2]
[3]
[4]
1.復習[1][2]
ユークリッド平面に三角形を描こうとします。ただし3辺の長さは隣接する3つの異なるフィボナッチ数であるとします。
このとき、フィボナッチ数の性質から、最も長い辺の長さは、ちょうど他の2辺の長さの和となり、三角形は描けなくなることがわかります。
では、曲率を有限値に、特に正にすれば良いだろうと考え、三角形を描ける球を前回、探しました。
2.今回考えたいこと[3]
前回の記事にて、隣接する4つの素数の関係式を、2つの側面から考えました。結果、次の2つの関係式を満足するだろうことが推察されました。
また、2つの関係式について、互いに何らかの関係性があるだろうこともわかりました。

予想1

予想2
2つをδを用いて次のような評価を行いました。

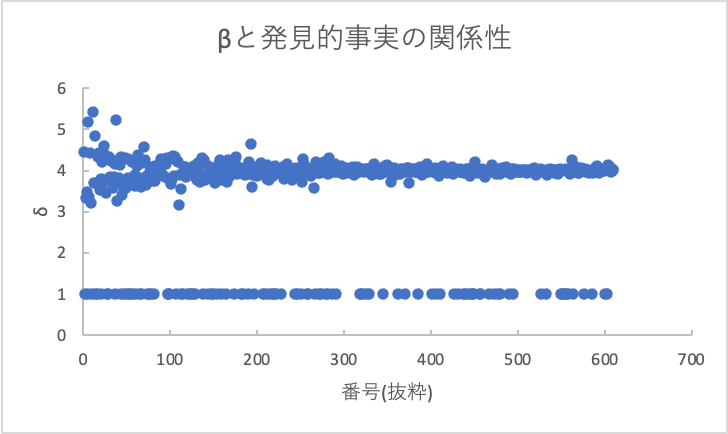
なぜか、4に近い値をとるという関係性を持つのです。
そこで、一旦、予想1を考察することを考えます。
3.隣接する4つのフィボナッチ数の関係式
予想1を変化すると、次のようになります。

これから類推して、フィボナッチ数について次のような式を考えました。

nを無限大に発散させるとどうなるかを考えます。
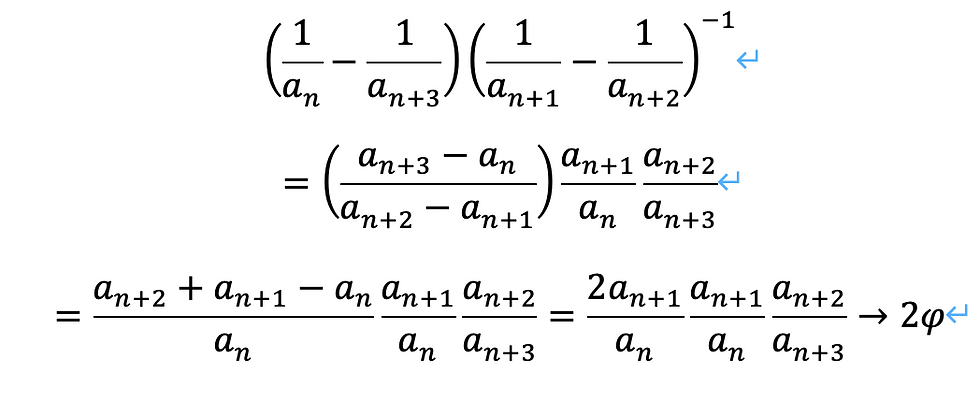
黄金比の2倍になることがわかりました。
そこで、次のように定理を与えることができることがわかります。

数値実験により、次の収束値を与えることがわかります。
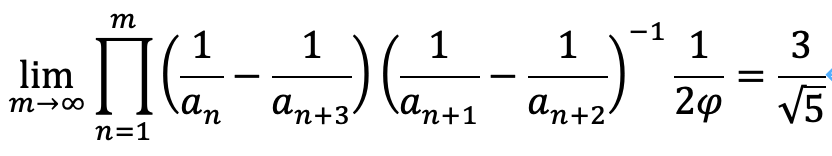
次のような計算を考えることができます。
(A)石音(不正解)
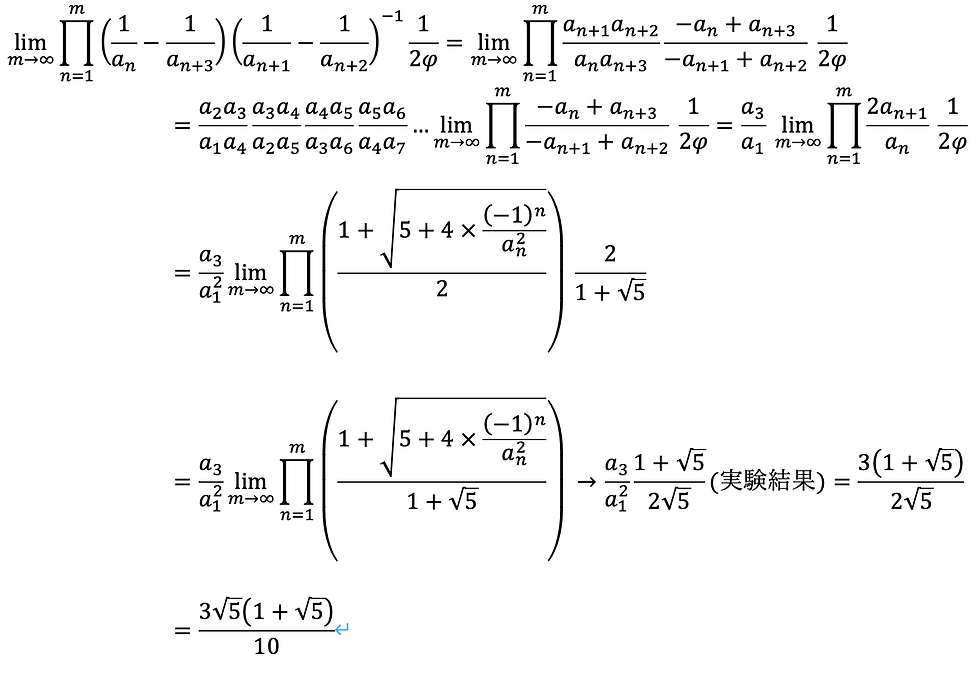
(B)戸松村の方法(正解)

4.隣接する4つの素数の関係式
隣接する4つの素数の関係式を考えます。
この無限積の数値結果は次の通りです。

なぜか160の4乗根にかなり近似することがわかります。
次のように表記することとします。

このとき、無限積の表記は次のようになります。

演算子を辺、数を頂点と対応させ、次の図形を考えることができます。

すると、頂点の数を変更することなく、鎖を作れることがわかります。
(奇数番号の面: 連続的に連なっている。偶数面: 4s+2は手前側、4sは奥側に、交互にくる)
頂点に数をふり、小さい順に回転(rot)を与えると、右ねじの法則から奇数番号面は交互に上→下→上→下となります。一方、偶数番号面は同じ方向を取ります。
偶数番号面は、面が手前→奥→手前…と振動することを、奇数番号面は法線ベクトルが振動することを、頂点にふった数が、大きい順へ移動する方向が一定であることを踏まえると、まるで電磁波のように見えてきます。
つまり、隣接する4つの関係式をある種の図形に考え連ねると、電磁波のようなものを描けることがわかりました。
以上の結果は、もしかしたら素数をなす空間はある種の電磁波が直線で進む空間、すなわち我々の生きている空間と相似であると推測することができます。
ところで、今回作った無限積と同様にして、フィボナッチ数で考えた場合はどうなるでしょうか?
このとき、黄金比の2倍で割り、かつ引き算を考える必要があったので、素数とは異なる振る舞いをするだろうことが推測できます。
5.サイクル論[4]
ところで、サイクル論によれば、i系ループとj系ループを考えることができました。そのサイクルの積を取ることにより、素粒子の基本構成を与えることができることを考えました。
その観点から推測すると、4章で考えた鎖は、i系ループとj系ループを直交させた図形の連続体であるとも捉えることができます。つまり、({{1 4}{2 3}},+)は、ある意味で素粒子であるとも捉えることができるでしょう。
6.素数とフィボナッチ数との違い
そもそも、素数の場合は、符号が+であり、フィボナッチ数の場合は、符号が-でした。
このことは、隣接する3つのフィボナッチ数を辺に持つ三角形は、曲率が正の有限値でないと描けないことと関係するかもしれません。
また、符号を-にした上で、黄金比の2倍でわる必要がありました。
その点から、構造的に異なるのだろうと推測します。


コメント