三角形の3辺がフィボナッチ数であるような三角形は、どのような曲面に描けるだろうか？(1)ユークリッド平面と球面の場合

0.参考文献

[1]http://horibe.jp/PDFBOX/SphericalTriangles.pdf

[2]https://manabitimes.jp/math/946

1.ユークリッド平面においての、三角形の3辺がフィボナッチ数であるような三角形

ユークリッド平面では、三角形の成立条件として、辺の長さに関する、次の関係が与えられています。(b_1, b_2, b_3, i≠j≠k)

これが、任意の辺に対していつでも成立するとき、このような長さの組み合わせで三角形を描くことが可能となります。

ところが、フィボナッチ数の定義式から、

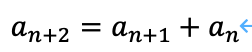
となります。これは、ユークリッド平面では線分でしか、このような3辺により"三角形"を描くことはできないことを意味します。"三角形"の定義を、「線分で平面に対して境界を生じさせ、3つの角が存在し、その境界面積は0より大きい。」とすれば、線分は三角形とは言えません。

定理1: ユークリッド平面において、三角形の3辺がフィボナッチ数であるような三角形は存在しない。

2.球面の場合

そもそも、前回の記事「フィボナッチ数列の三角関数(tangent)を用いた漸化式」を書く上で、考察しようとした時、球面ではきっと三角形を描けるだろうと考え、この場合に球面上での正弦定理と余弦定理を用いて、関係式を導出しようとしていました。しかし、どうしても数値実験結果と理論結果が合わないので、「そもそも三角形は描けないのではないだろうか？」と考えたわけです。どうなのでしょうか？見てみましょう。

2.1 球面の三角形の面積[1]

一般に、以下の公式が成立します。面積をS、半径をR、三角形の内角をA、B、Cとしています。

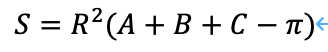
3辺の長さをフィボナッチ数(a_n、a_(n+1)、a_(n+2))とするために、半径を次のようにします。

こうすれば球の断面、特に半径がRの時、四分円の弦の長さがa_(n+k)となります。

kについての評価を考えます。

また、a_(n+k)が3辺より小さい場合を考えます。すると、懸念すべきは辺の長さが半径Rに対してπRより小さくなっている必要があることです。そもそも三角形は、線分(=最短距離を結ぶ線)で囲まれている図形ですから、この条件が必要です。

すなわち、

以上から、k=1であることがわかります。

この時の面積は容易に求まります。

偶然ですが、ひとつ前の記事でも4/πが出てきましたので、せっかくなので次のように整理してみます。

あるいは、次のように書くと美しいですね。