三角形の3辺がフィボナッチ数であるような三角形は、どのような曲面に描けるだろうか？(2)一般な単連結3次元形状の場合

0.参考文献

(1)と同様

[1]https://ja.wikipedia.org/wiki/楕円体

1.復習

(1)では、半径が(2a_(n+1))/πである球面においてのみ、(a_n、a_(n+1)、a_(n+2))を辺の長さとする三角形が描けることを示しました。

ここで、ひとつ訂正、あるいは注意すべきことがありました。正確には、半径が以下の範囲である球面であれば、可能です。

ですからより正確には、「半径を通る球の断面にあたる円について、その四分円の弧が自然数となるよう設計する」と言う制限を与えるべきですね。

2.楕円体化

次に、三角形の面積が最大となるように、球を連続変形させます。以下は予想です。

「任意のn次元平面に対してn次元(楕)円を描いたとき、この(楕)円に内接する三角形について、全ての内角は等しいだろう。」

この予想が正しいと仮定した時、辺の長さが(a_n、a_(n+1)、a_(n+2))であるような三角形で、面積を最大にさせる平面は、次の式で表せる楕円体となります。

こうすれば、全ての内角が90度の三角形ができます。

この楕円体の正規化体積(本来の体積に対して、R^3で割ったもの)は次のように求まります。

nが十分大きい時、確かに楕円体の式は異なりますが、体積は一意に定まります。ζ(2)=(π^2)/6に対して、π^2ζ(2)=Vとなるのが面白いですね。

元の体積は、正規化されているので(4π/3)ですから、

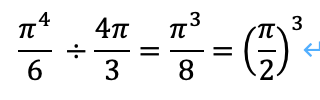
となり、(π/2)^3倍大きくなっていることがわかります。

3.楕円体に描かれた三角形の面積においての最大値

自明な最大値(a_0)=∞は、実際は「辺の長さ0」を考えているために起こります。これは不適ですね。

では、Vをnで微分して、0に等しくなる値を考えましょう。

簡単のために複素数を使って計算しました。結局、フィボナッチ数を与える数列の"極大値"を取る必要があります。

一見すると自然数の範囲には解がないように思えます。複素数に拡張して考えましょう。

ビネの公式を微分して整理することで、nについて求まります。計算結果は以下のとおりです。

やはり、自然数解は存在しませんでした。

第二項が減衰振動項となることから、nが小さいほど値は大きいことがわかります。よって、n+1=3の時、最大値を取ります。

20.293...となります。

4.表面積

4.1 正規化表面積

では、この時の正規化表面積(本来の表面積に対して、R^2で割ったもの)を求めましょう。実は、楕円体の表面積を求めるには難しい積分(第一種および第二種楕円積分)を与える必要があります。

ところが、誤差が最大でも1.061%に抑えられるような近似式が存在して、次のようなものになります。p=1.6075

以上から、表面積は次のように求まります。

4.2 元の球の場合と比べて面積は何倍か？

球についての表面積は次のようにもとまるのでした。(前回の記事とは違い、正規化してあります。)

これより、何倍かと言うと、

この数字を見ると、ルート5にちょっと近いのでは？(表面積の公式自体にも誤差があるし…)と気付きますね。

実際にWolfram alpha で計算させてみると、相対誤差はわずか0.4903%になることがわかります。

以上から、nが十分大きい時の、楕円体に描かれた(面積最大の場合の)三角形の表面積は、

で求まるだろうと予想できます。