「レンズ」βの厳密な評価について
- S Y
- 2022年12月10日
- 読了時間: 2分
更新日:2022年12月20日
0.参考文献
[1]
[2]
1.復習
前回の記事で、素数の4項間関係式について、以下の関係にあることを考えました。


前回の記事にて、β_(0123)がほとんど1に近い値をとることを示しましたが、これはA(n)が1であることを仮定したものでした。(あるいは、A(n)の数値実験値を代入した結果のものでした。)
ところでβ_(0123)は、スライムの理論をもとに考えたものなので、この値は本質的に重要です。そこで、A(n)に依存しないβ_(0123)の評価を、今回は考えていきます。さらに、このβ_(0123)に対しても、4つの素数との別の関係性を数値実験により予想を示し、4つの素数だけで評価する式を示します。また、-1/2+itの形が途中で現れたので、この点について考察をします。
2.A(n)の定義式(θの定義式)
前回の予想にて、nに対するAは一定値を取るだろうと考えました。そのAは実際は、nが小さい、特別な場合を除いて一定値であることが数値実験によりわかりました。
ところで、その結果をそのまま使うことにより、β_(0123)を数値実験により考えましたが、もしA(n)を使わなければ、より正確なβ_(0123)の値を算出できるだろうことがわかります。
さて、A(n)の定義式を代入することで、β_(0123)の厳密値を表せるだろうとわかります。また、θの定義式を代入すればよいことがわかります。
θの定義式は次のとおりです。

3.θの定義式を、β_(0123)についての式に代入する。
tan(θ)、sec(θ)について求めます。

これらを代入すれば、次のようになります。

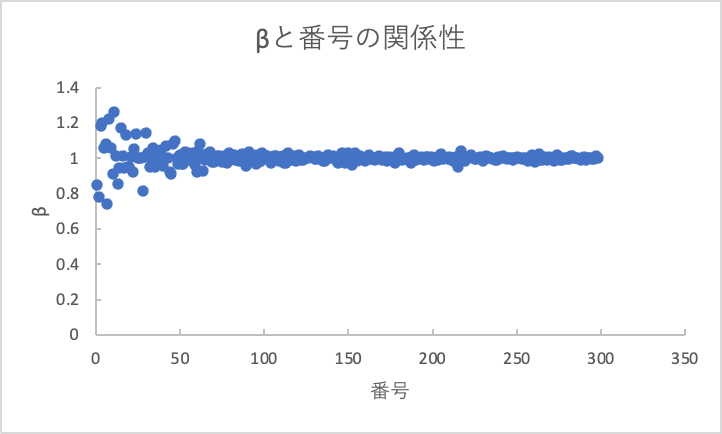
実際、数値実験結果はこのようになります。1に近い値を取ることがよくわかります。
4.4項間の関係式について、足し算と掛け算の関係性を考える
次の事実を発見しました。これは、βの定義式から容易に想像することのできる事実です。

次のようになります。
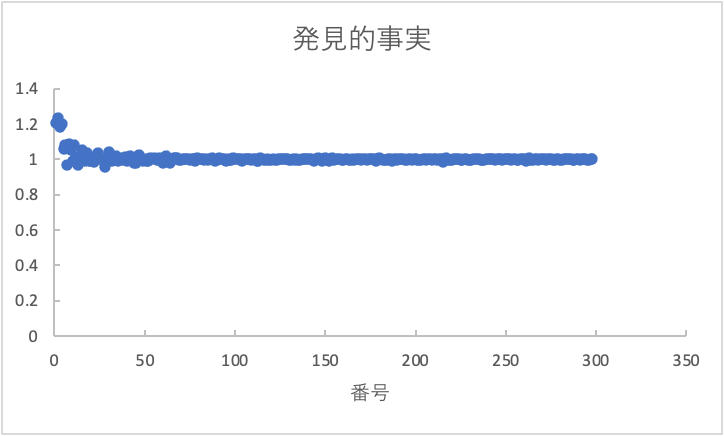
βと発見的事実は非常に類似した関係性を満たしているように見えます。
そこで、次の評価を与えます。

このδの推移をグラフにしました。
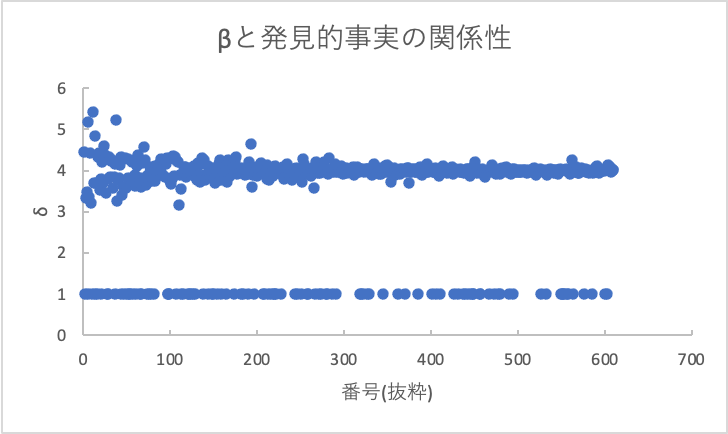
結果、1倍の時か、約4倍の時かの2通り存在することがわかります。
5. δ=1の時


δ=1とは、予想が完全に一致していた場合のことです。つまり、x=1を意味します。ところで、解の範囲を複素数まで拡張すれば、実部が-1/2になることがわかります。このことは、ゼータ関数の零点の実部が1/2になることと、もしかしたら関係があるかと思います。
6. δ=4の時

このような関係性を満たすことがわかります。


コメント