素数からなる数空間において、スライムのワイセンベルク現象から導出したブラックホールの式が、オイラー・ラグランジュ方程式であった時、数空間を通信するのに必要な「レンズ」について、定量的に求める。
- S Y
- 2022年11月29日
- 読了時間: 2分
0.参考文献
[1]
[2]
1.復習
古典力学をもとに、ブラックホールを成した連星系の、それぞれの星の質量に基づいた静止エネルギーe1とe2について、以下の関係式が成り立つことが以前の研究によりわかりました。

また、隣接4項間関係式についても以下の結果を以前の研究によりわかりました。

2.オイラー・ラグランジュ方程式
オイラー・ラグランジュ方程式は次のように与えられます。

ここで、q_iは一般化座標です。
3.ブラックホールの式は、ラグラジアンか?
ラグラジアンを仮定して比較すれば、次の関係式が考えられます。

この結果からラグラジアンについて、次の関係式を得ます。

ここに、Lは等しいため、次のように考えることができるでしょう。
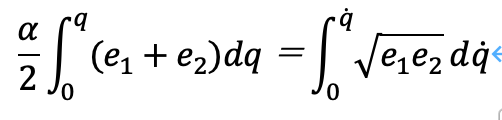
ここに、静止エネルギーが数そのものであると考えた場合、次のように考えることができます。

この2つは、前者はp(n)とp(n+3)の2つの「星」からなる宇宙について、後者はp(n+1)とp(n+2)の2つの「星」からなる宇宙についてのブラックホールを説明しています。
以上を整理すれば、次のような結果を得ます。

以上から、素数の倍率βについて、次のように考えることができます。

4.αとβについて
非線形空間である数空間、sqrt(e1e2)の時間微分が、線型空間となることが、ブラックホールの式の本質でした。ところで、その微分量の「倍率」は数e1とe2によると考えられ、それこそ、αであると考えられます。
ちょっとわかりにくかったですね。つまり、サッカーボールで説明すると、こうなります。ボールの形状は明らかに非線形です。一方微小範囲では、正五角形、正六角形の平面となります。平面では、線型空間となります。また、非線形なサッカーボールを作り出すためには、正五角形、正六角形の倍率が常に一定でなければなりません。この倍率こそ、αなのです。
この変換に必要なαが、もし別の数空間へ移るときに変換され、別のαとなったとき、この変換の倍率をβとします。つまり、「変換作用素α」に対する倍率がβなのです。
イメージは、サイズの異なるサッカーボール同士の変換といったところでしょうか。
5.数値実験値
実際に計算したところ、ほとんどいつでもβ=1であることがわかりました。


コメント