古典力学による、ブラックホールを含む時空のスライム的性質の解説(相対論による静止エネルギーを一部使用)
- S Y
- 2022年9月26日
- 読了時間: 5分
更新日:2022年10月2日
[2]
[3]
[4]
[5]
[6]
[7]
1.シュワルツシルト半径[1]
ブラックホールに対して、質量mの物体に対して運動エネルギーとブラックホールによるポテンシャルエネルギーの釣り合いを考えます。すると、あらゆる物体が脱出できないようなブラックホールからの距離が存在して、以下で与えられま
まずは、光速で運動する質点の持つ運動エネルギーが、巨大星のポテンシャルエネルギーと釣り合ってるのは、以下の式で表せます。

もしこの半径より近ければ、光速を超えないと脱出できなくなります。ところが、相対性理論によれば、任意の物質は光速を超えることはできないとされます。よって、ある距離r_c以下に近づいた物質を吸い込んでしまうのです。
そのような半径r_cを、シュワルツシルト半径と呼びます。

もし、静止エネルギーを考えるならば、次のように考えることができます。(E=Mc^2)

2.ブラックホールの「角速度」次に、ブラックホールでないが、合体すればブラックホールとなるような連星を考えます。簡単のため、2つの星で考えます。(M=M_1+M_2, E=E_1+E_2)
この時、合体してできるブラックホールのシュワルツシルト半径ギリギリの系を考えます。(近似的に等速円運動を考えています。)
2つの星に対して、万有引力と等速円運動がほとんど釣り合ってると考えます。

角速度は次のように表せます。

ここに、シュワルツシルト半径の定義から、次のように整理することができます。

これが、ブラックホールとなる直前の連星系の角速度です。(石音角速度)
3.角運動量[2]
スライム(というか、レオロジー)は、ワイセンベルク効果が発生します。
おそらく、以下のように説明できると思います。簡単に説明すれば、スライムを分子的に見ればゴム性の連続鎖と考えることができるので、軸の回転により摩擦熱が生じ、張力が上昇することで、スライムが上昇するそうです。
すると、角運動量を考え、その変化を考えると良いだろうことがわかります。
回転する剛体の半径をシュワルツシルト半径、角速度を石音角速度とします。ブラックホールの取り込む流体の質量をmとすれば、次のように考えることができます。

この時、トルクFについて、角運動量の時間微分であることから、次のように表せることに気づきます。

ただし、第一項は時空をスライムの性質を持つ流体と捉えた場合の、トルクが生じる箇所の質量変化を意味しています。第二項及び第三項は、ホーキング放射などによる、ブラックホールの元となった連星のそれぞれの質量の時間変化を意味しています。
4.ゴム弾性、及びブラックホールの熱力学[3][4][5]
ゴムは、荷重をかけることで伸び、除荷すれば元に戻ります。この原理は実は、エントロピー弾性を考えることで説明できるそうです。
ゴムの温度をτ、長さをlとすれば、張力Fは次のようになります。

エントロピーについて、ゴムの長さ変化を考えることにより比例定数が現れ、その時点のゴムの温度と積を取れば、これが外力となることを意味しています。
ところで、ホーキングによれば、ブラックホールの熱輻射は次の式で表せます。

また、エントロピーはベッケンシュタインとホーキングによれば、次の式で表せます。

張力について、次のように表せることに気づきます。

5.角運動量の変化(トルク)とブラックホールの熱力学によるゴム弾性との関係
トルクの次元は、[N・m]なので、代表長さで割ることを考えます。この系において相似変換可能な長さは、シュワルツシルト半径ですから、これで割ります。
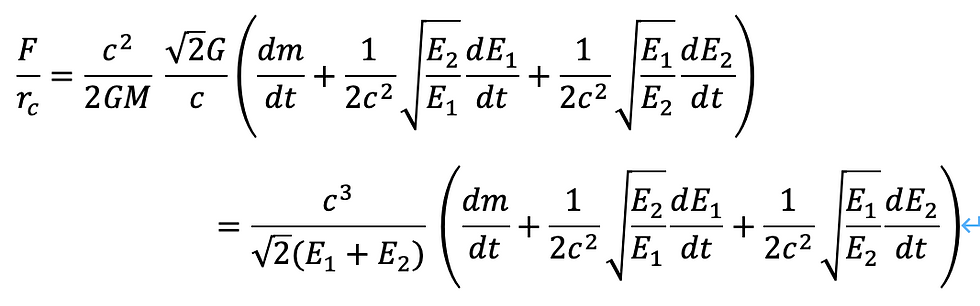
一方、4章の議論から、最左辺は張力と等しいことがわかります。(ゴム弾性の張力と、トルクは釣り合うことを意味しています。)
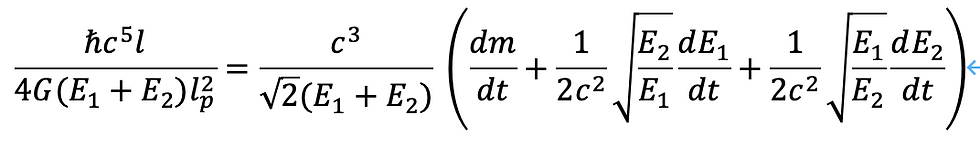
これを整理すれば、次のようになります。
以上をdm/dtについて解くと、次のようになります。
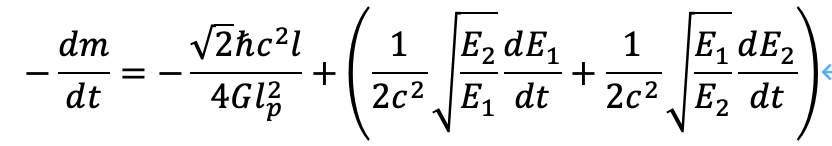
ホーキング放射を考えると、右辺第二項及び第三項の時間微分について、負となることがわかります。
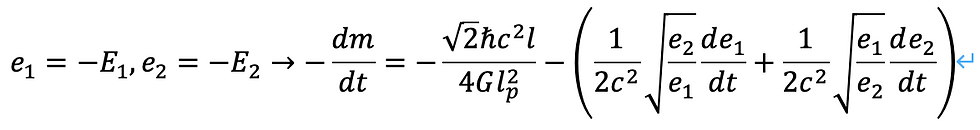
特に、l=r_cを考えます。
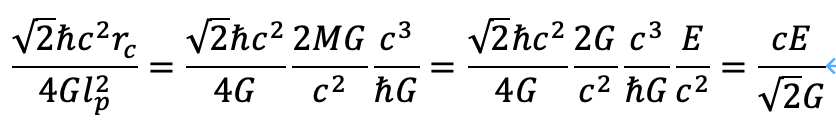
さらに、dm/dt=0であると仮定すれば、次のように整理することができます。
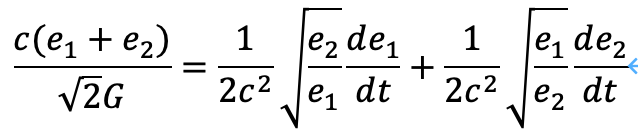
6.電磁気力に関する議論
電気に関するクーロン力と、磁気に関するクーロン力について、同様に考察しますと、次の結果を得ます。
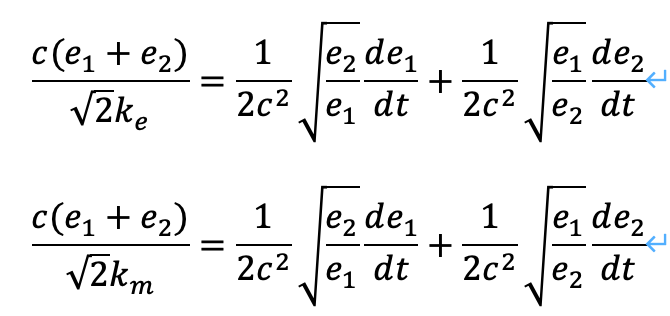
両辺についてそれぞれ互いに割ると、次のようになります。(式A)
ここで、添字のeはelectro, mはmagneticを意味します。
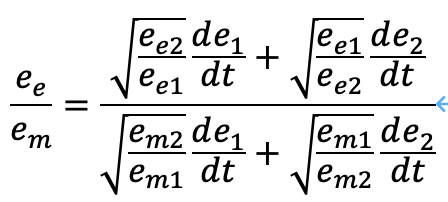
ところで、電磁波について電場の振幅と磁場の振幅の比は以下で表せます。

波についてそのエネルギーは振幅の2乗に比例するため、一般に次のようになります。
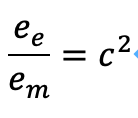
すると、確かに式Aは正しいようであることがわかりました。
つまり、電磁場について、ブラックホールの取り込む流体の質量は常に一定であることがわかります。
電場と磁場は互いに直交する性質を持ちます。
そこで、特異ベクトルが円形をしているとすれば、電場はその周囲を纏うようになり、トーラスの形状をしていることとなります。
さらに、そのトーラスについて、軌跡を円形とした場合、連続体もまた、トーラスとなります。そうすれば、ある意味で直交であるといえます。
まとめ
電場: 磁場トーラスの連続体であり、トーラス
磁場: 電場トーラスの連続体であり、トーラス
7.重力について
先の式を再掲します。

これを整理すれば、次のようになります。(2022年10月2日訂正 正しくは、<2>のことです。これ以下の議論は、この修正をする必要があることを以て、読んでください)
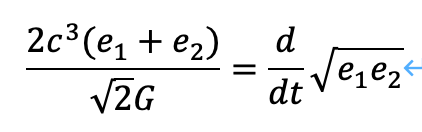
<2>

二項和の二乗を考えると、次のように変形できます。

ここに、右辺を整理すべく、次のように考えることができます。

以上から、次を得ます。

8.サイクル論の観点からの考察[6][7]
サイクル論によれば、ある行列変数が存在し、以下の式が成立することが知られています。
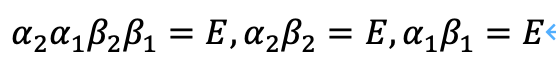
行列の場合も、複素数を値にもつ変数であるときと同様に次の式が成立すると仮定します。
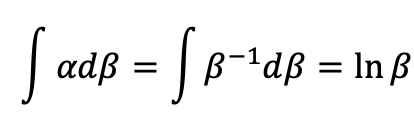
すると、以下の式が成立することがわかります。

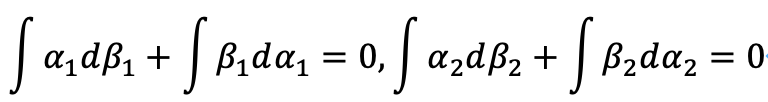
これは、サイクルの中に特異ベクトルが存在しない場合に成り立ちます。
ところが7章の結果は、特異ベクトルが存在するときを示しています。言い換えると、以下のことがわかります。
1 静止エネルギーは実は、サイクル論の行列に相当すること
2 特異ベクトルの周りでのサイクル論を考えると、時間変化する何らかの値をもつこと
1番については、特に次のサイクルを一般には考えることができるだろうことを期待させます。

ところで、サイクル論によれば、次のようになることがわかっています。
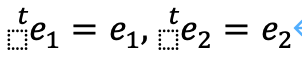
つまり、この時空には、実は直交している時空があるが、直交してるがゆえに見えないことを示唆しています。
すると、以前の記事で議論した、虚世界の概念を捉えることができます。[7]


コメント