スライムの回転上昇現象の説明 その1

0.参考文献

[1]https://youtube.com/shorts/RHyNfexjIRQ?feature=share

(9/23/2022 2:28 追記) [2] https://www.jstage.jst.go.jp/article/jsms1952/6/43/6_43_227/_pdf

↑全く同じ研究が、先行研究としてありましたので紹介します。

1.動画の解説[1]

動画では、垂直にストローをスライムにたてたまま、ストローを、中心軸を回転軸として回転させました。すると、図1のようにストローにまとわりつきながら、ネジのように上昇していきました。

図1 スライムの上昇現象

謎は2点あります。(1)スライムの上昇機構の説明、(2)上昇に必要なエネルギーと角速度の関係式

今回は、(2)を説明する仮説について提唱します。

2.剛体壁と剛体丸棒の間に成り立つ、トルクと変位の関係

次のような2つの剛体が接続した場合を考えます。

図2 剛体壁と剛体丸棒の関係

ただし、剛体丸棒と剛体壁は接していて、滑らないとします。

また、剛体丸棒の質量をm[kg]、長さをl[m]、断面は円、この直径をd_0[m]、重力加速度g[m/s^2]は剛体丸棒の回転軸に平行、かけるトルクはT、ただし、

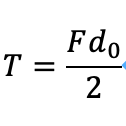
式1

とします。ここでFは剛体丸棒を角速度ω=const.で回転するときの力に等しいとしますから、

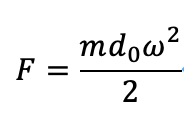
式2

となります。式2を式1に代入すれば、次のようになります。

式3

ここで、丸棒についてのFBDを考えます。

図3 剛体丸棒のFBD

図から、反力R_0=-mg、トルクはT_0=-Tであることがわかります。

今回の問題では、特にトルクについてのみ考えたら良いです。

3. トルクT(x)とその時間微分

剛体壁と剛体丸棒の接平面から、鉛直方向にx軸を取りますと、xでの仮想断面について考えることができます。すると、トルクT(x)がわかります。

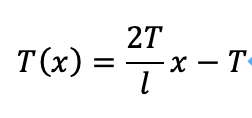
式4

ここで、T(x)に対して時間微分を考え、角速度を用いて表します。Tが定数であることに注意すれば、次のようになります。

式5

4. ストロー1回転分に対するスライムの上昇量と、それに必要な位置エネルギー変化

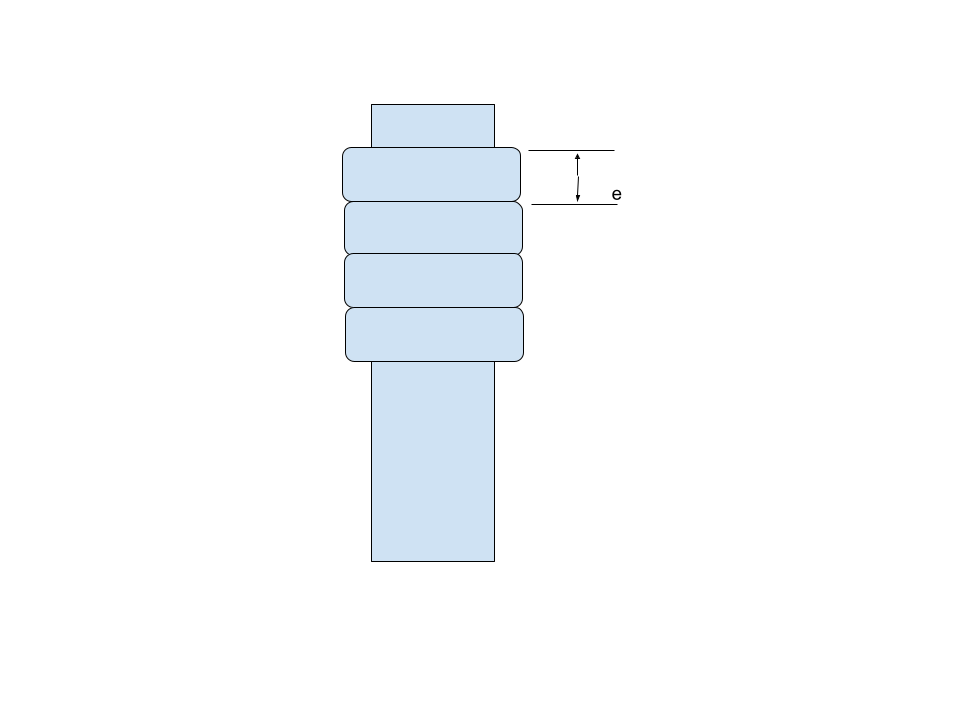
図4 eの定義

動画によれば、十分回転した場合、ほとんどのスライムはネジのように等間隔に、かつ同じ太さで巻き付いているのがわかります。この太さをeとします。eは次のように定義することができます。

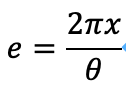
式6

θは回転角です。すると、時間微分は、次のようになります。

式7

ここで、スライムの物性をまとめます。

ρ[kg/m^3]: 密度

V+W[m^3]: ストロー1回転分で新たに上昇に加わるスライムの体積

V[m^3]: 円筒形部の体積

W[m^3]: 円筒形以外の部分の体積(表面張力などによる曲面部を含む部分)

さて、n回転目における、スライムの位置エネルギー変化を考えます。

式8

この変化は、剛体丸棒を1回転させた時にかけたトルクに等しいですから、次のようになります。

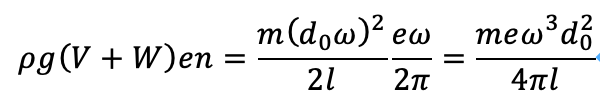
式9

次章では角速度がどのような物理量に関係するのかを知りたいので、角速度について解きます。

5. 角速度の関係式

5.1 体積計算

W~0と近似します。Vは円筒なので、次のように計算できます。ただし円筒の直径をd(=d_0+δ)とします。

式10

5.2 角速度ω

式10を式9に代入したのち、整理すれば、次のようにもとまります。

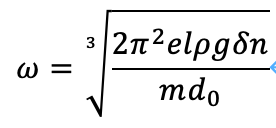
式11

これが、n回転目に必要な角速度です。

6.展望

粘性係数などの流体力学パラメータを用いてeとδを表したいです。