粘弾性のマクスウェル=フォークト統一モデルが無限個接続された場合、モデルはどうなるか?
- S Y
- 2023年1月6日
- 読了時間: 4分
更新日:2023年1月9日
次の記事にて、修正されています。併せてみてください。
0.参考文献
[1]
[2]
[3]
1.復習[1]
粘弾性体(スライム)の運動は、マクスウェルモデルや、フォークトモデルが考案されています。これを力学的相似から、相似な電気回路を考えました。
さらに、相似な電気回路について、線形接続することにより、記事[1]の、マクスウェル=フォークト統一モデルを考えました。
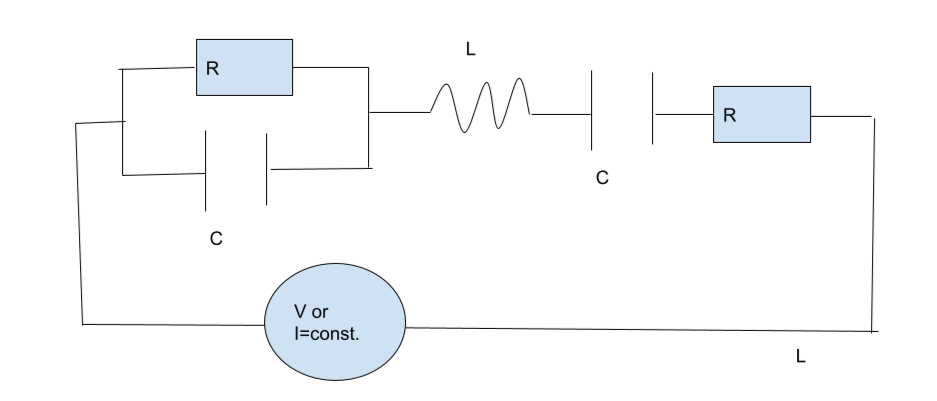
ところでこの系は、粘弾性体のある微小領域においての運動方程式です。ですから、実際の系は、この統一モデルを無限に接続させるモデルとなります。

ただし、MVはマクスウェル=フォークトモデルのことです。今考えた、RC並列接続と、L, C, Rの4要素直列接続のことです。
今回は、このモデルを考えます。
2.無限接続統一モデルの特性について
この運動方程式は、次のようになります。ただし、q2はRC並列接続における、コンデンサに流れる電流d(q2)/dtのことです。
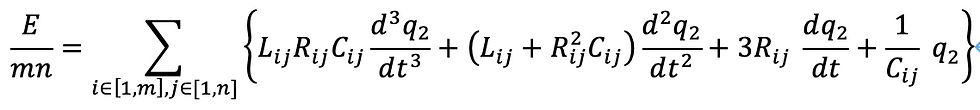
このままmとnを無限大にした場合、左辺は0となります。ということは、このモデルは正しくないことがわかります。
まずは、計算しやすいように、m=nとします。

nを無限大に発散させる操作をしつつ、有限値を与えるためには、次のように考えます。
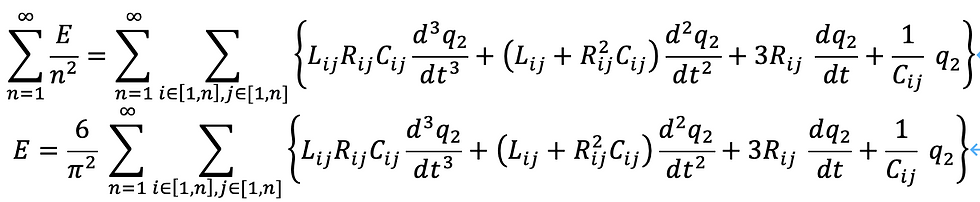
これは、次の回路のことを考えています。
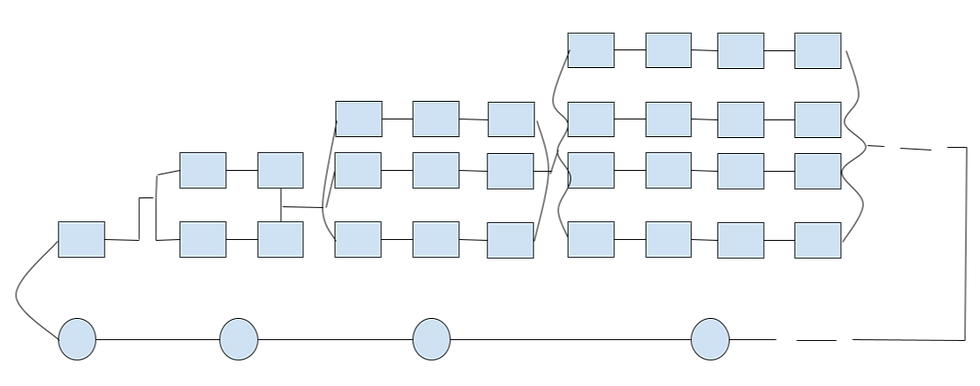
○は入力電圧E、□は統一モデルです。それぞれの統一モデルにLij、Rij、Cijという、物性値を持っています。
特に、粘弾性の性質が任意の配位空間において同一である場合、物性値は常に等しいため、方程式は次のようになります。
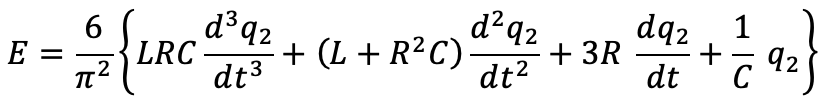
この方程式は、統一モデルの場合に対し、外力のステップ応答がζ(2)倍されていることがわかります。
3.無限接続統一モデルの特性について(II) [2]
2章では、m*nのモデルを考えていました。
これを、N次空間における場合と考えます。さらに、モデルの個数はある次元に対していつでもnとなると仮定します。
この時方程式は、統一モデルの場合に対し、外力のステップ応答がζ(N)倍されていることがわかります。
すなわち、次のように考えることができます。

ところで、以前の記事で、tangentとゼータ関数の関係式を示しました。これより、次のように求まります。

特にx=q2で、Eがq2の1次に比例することは、前回の記事で仮定したことと合致します。
ここで登場するxは、q2と性質が異なります。
q2…局所座標系の一般化座標の意味。離散化可能(量子化可能)
x…ある種の連続性を意味する、外力の性質を持つ変数。このxによる外力を共通して持っているもの(すなわち、外力Eを共有するもの)は、粘弾性として連続していることを意味する。連続性は、接続球から分離球への変換において、完全に分離球になる直前で説明できるでしょう。
(2s)次空間の場合、式は次のようになります。

ここに、係数Eが比例制御(qの(2s-1)次制御)を意味すると仮定すれば、次のように書き換えることができます。

右辺に、1+1+1+...の項が生じます。これは-1/2に等しいのはよく知られていますね。すなわち、以下のようになります。

また、粘弾性の性質が任意の配位空間において同一である場合、物性値は常に等しいため、方程式は次のようになります。

この斉次方程式は、前回の記事[1]の通りです。
特解を考えます。
4.特解[3]
そもそも、ここでxとは、外力が共通して働いていることを意味する変数であり、ある種の連続性を説明するものでした。(連続体仮説)
一方、q2とは、一般化座標のことを意味し、離散化されているのである意味で量子性を説明するものでした。(量子仮説)
この方程式は、量子性と連続性の両方を説明するものと考えられます。
xは、定義からq2や時刻の変数ではないだろうと推測できますので、定数項であると仮定すれば、次のように考えられます。

これは物理的には、量子性と連続性を意味するものです。
ところで、以前の記事にて、γ=tan(γ)の考察をしました。これを満たすγは整数kを用いて表される離散的量であることがわかります。


コメント