(修正版)粘弾性のマクスウェル=フォークト統一モデルが無限個接続された場合、モデルはどうなるか?
- S Y
- 2023年1月9日
- 読了時間: 3分
更新日:2023年1月10日
0.参考文献
[1]
[2]
[3]
[4]
1.復習[1][2]
前回の記事で、次の方程式を考えました。これはN次空間における統一モデルの無限接続を考えた場合の式です。
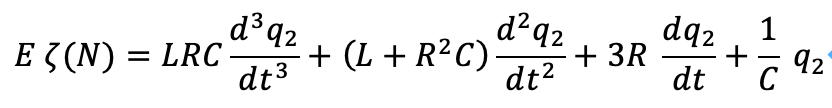
特にN=2sとした場合、ζ関数に対して無限和を与えることにより、tangentに変換することがわかっています。ただし、Eは次のような仮定をします。
仮定A

この仮定は、前回はtではなくxとしました。すなわち、外力は時間や座標に関係ない何らかの変数によって変換すると考えたのです。
一方、今回は時間tの関数であると考えました。この仮定は、スライムのワイセンベルク現象において、ストローの回転数が時間に比例し、ストローの回転数が大きくなるほど、トルクを大きくする必要が生じるため、このように考えられるだろうとしたのです。係数は、ζ関数をtangentにするためにうまく辻褄を合わせました。
2.ロンスキアンの解説[3]
n階の線形微分方程式において、ロンスキアンは次のように定義されます。u_iは微分方程式の斉次解の一つです。
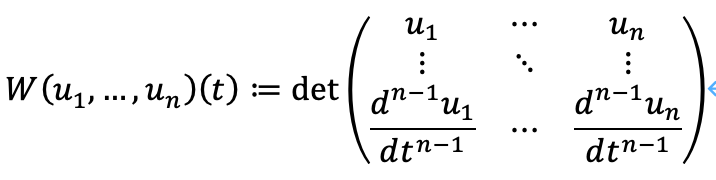
この行列式が0であれば、線形従属であることの必要十分条件となります。
これをうまく使うことにより、特殊解を求めることができます。
例題として、次のtについての微分方程式を考えます。

この微分方程式の特性方程式の解は、三重解となります。斉次解は次のようになります。

これで、全ての斉次解を表せます。
本当でしょうか?本当です。この証明方法は、ロンスキアンが0とならない、すなわち線形独立であることを示すことから説明できます。
非斉次方程式の右辺項Q(t)を考えると、未知係数について、次のようになります。
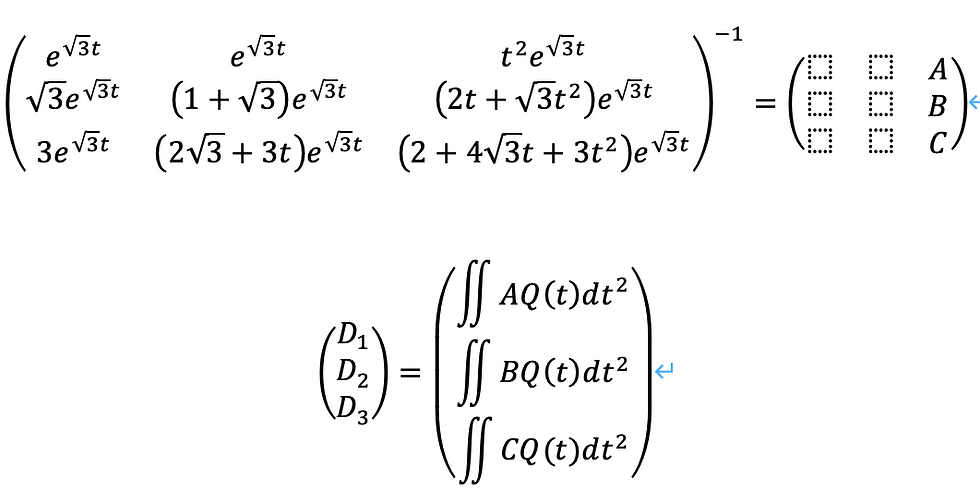
これを仮定した上で、次のように特殊解を考えることができます。

3.仮定Aの場合の微分方程式の、解の導出[4]

仮定Aの場合、微分方程式は上のようになります。右辺の係数の場合、3重解を考えることはできません(そのようなL, R, Cは存在しません)。そこで、3つの異なる解を持っていると仮定します。解を、λ_(1、2、3)とします。
3.1 ロンスキアンの行列
ロンスキアンを考えるために、次の行列を考えます。
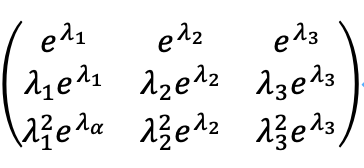
この逆行列は、ガウスの消去法を用いることにより求めることができます。次のように求まります。

未定係数は次のようになります。
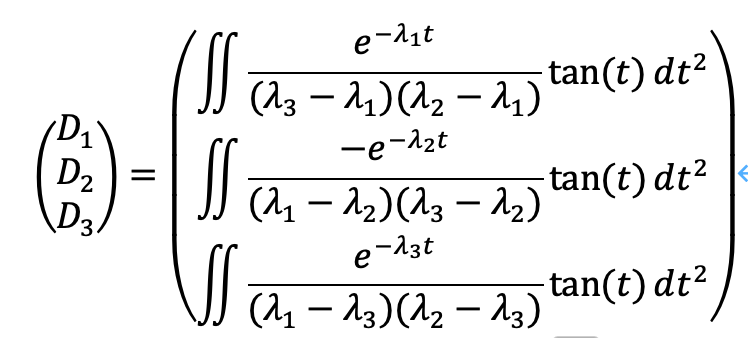
3.2 ある2階積分の解
次の2階積分を考えます。

まず、1階積分を解きます。

初等関数で考えることはできません。Wolfram Alphaで解いてみましょう。

なんと、超幾何関数が現れてしまいました。この積分はきっと難しいでしょう。でも大丈夫。我々にはWolfram Alphaがついています。計算してもらいましょう。

残念ながら、計算してくれませんでした。残念。自分で計算しろと怒られてしまいましたね。(本当は、超幾何級数の積分を計算してくれないだけです。)
今は、超幾何級数の積分を考えます。
そもそも、超幾何級数は次のように定義されています。

ここで、(x)_iはポッホハマー記号と呼ばれるものです。以上を用いて、次のように表せます。

それぞれ積分すると、次のようになります。

ここで、新しい超幾何級数を考えます。名付けて、石音夢超幾何級数です。

これを用いると、次のように求めたい2階積分の解を与えられます。
(訂正 2023/1/10 10:23 exp(2int+iπ)は、exp(2int+iπnが正しいです。)

3.3特殊解
特性方程式の3つの異なる解はλ_(1,2,3)です。(α.β,γ)を(1,2,3)でサイクリックに、非復元抽出で(アインシュタインの総和規約と同様にして)、特殊解は次のように表せます。

。


コメント