素数の世界を説明するスライムを、粘弾性体とみなした場合、マクスウェル=フォークト統一モデルにおける各種パラメータの値は幾つになるか？

0.参考文献

[1]

[2]

[3]

1.復習[1][2][3]

前回の記事にて、マクスウェル=フォークト統一モデルとなる、電気回路を紹介し、その振る舞いについて考察しました。

結局、次の方程式に支配されることがわかりました。

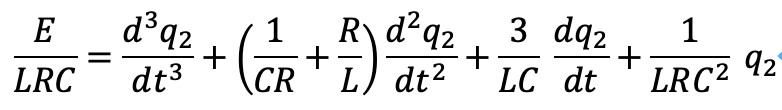
ところで、以前の記事にて、隣接する3つの素数を辺の長さにもつ三角形の共通点を探りました。結果、これらの角度についてある共通点があり、近似的にsqrt(3)という数字が、角度に関する三次方程式の3重解として生じることがわかりました。

今回の記事では、マクスウェル=フォークト統一モデルの3階微分方程式の特性方程式が3重解を持てば、素数の「宇宙」を粘弾性とみなした時の、宇宙についての方程式を説明できるだろうと考え、そのような空間に相似な性質を持つ、インダクタンス、電気容量、電気抵抗の値を探ろうと考えます。

2.斉次方程式の場合

まずは、斉次方程式であるとみなし(つまり、入力電圧がステップ、定常であると仮定し)、係数を比較します。

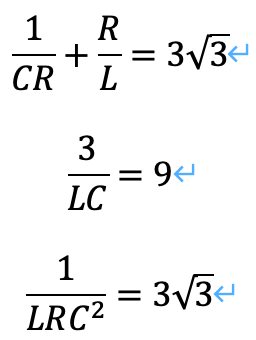
すると、以下の理由から、おかしなことが生じます。

1=2となり、どうやら0で割った時と同じことが生じることがわかりました。

そこで、次は入力電圧がq2についての比例制御となっていると仮定します。

3.非斉次の場合

方程式は次のようになります。

すなわち、次のようになります。

変数が4つに対して式は3つなので、L, C, Rは入力が比例制御である場合の比例定数Eに関する変数であることがわかります。

ちなみに、スライムのワイセンベルク現象において、変形を与えるようストローを回転するときに、回転回数に比例してトルクを大きくしていたので、比例制御は実際の現象との整合性が取れています。

この方程式を解くと、次のようになります。(解くときは、CRをaとおき、αの2次方程式を解いて整理するのがコツです。)

この結果から、Eが0ではいけないことがわかります。

また、各種パラメータの数値を与えることができました。

最新記事