粘弾性のモデル、マクスウェルモデルとフォークトモデルは、電気回路モデルのどのようなものと物理的に相似か？

0.参考文献

[1]

https://www.terrabyte.co.jp/discover/index.php/2019/12/17/post-1107/

1.マクスウェルモデルとフォークトモデル[1]

粘弾性流体には、ばね要素とダッシュポット要素の2つに大別できます。

ばね要素は次の関係式があります。

一方、ダッシュポット要素は次の関係式があります。

1.1マクスウェルモデル

ばね要素とダッシュポット要素の直列接続による物理モデルを、マクスウェルモデルと呼びます。

物理量は次のように定義します。ただし、縦であろうと横であろうと、式の形は変わらないため、今回は縦変形を考えます。

この時、運動方程式は、次のように定まります。

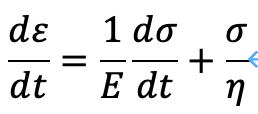
ステップ入力であるため、左辺は0となります。この斉次方程式の解は次のとおりです。

1.2フォークトモデル

ばね要素とダッシュポットモデルの並列接続による物理モデルを、フォークトモデルと呼びます。

物理量は次のように定義します。縦と横で式の形は変わらないので、今回は縦を考えます。

この時、運動方程式は次のように定まります。

斉次方程式を仮定した後で、左辺はt<0で0、t>=0でσであると考えます。

この方程式の解は次のようになります。

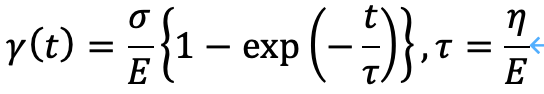
2.電気回路4つの候補

外力項(入力項)とインダクタンスLは直列につながっているとします。この時、問題はRとCが直列か、並列か、どちらになっているべきかを考えることが大切です。RとCの接続したものと、Lと外力項の直列接続と直列に接続することを考えます。

まずは、RとCが並列に接続されていることを考えます。外力項は直流電流か、直流電圧かの2通りあります。これをまとめて図1にしました。

図1 (a)V=const. (b)I=const.

同様に、RとCが直列に接続されていることを考えます。図2です。

図2 (c) V=const. (d)I=const.

以上、(a)~(d)の4つの候補について考えます。

3.4つの候補のキルヒホッフの法則について

以下の表にキルヒホッフの法則について、4つの候補に対してまとめました。

それぞれの微分方程式を解くことで、以下の結果を得ます。

5.マクスウェルモデルとフォークトモデルなどの粘弾性モデルと、電気回路モデルの比較

以下に、マクスウェルモデルの粘弾性モデルと、各電気回路モデルの比較をしました。

4つを比較すれば、2つは境界条件が誤っていたために、少々おかしなことが起きていることに気づきます。

モデルbは、入力が定常電流でした。これは、マクスウェルモデルの入力がひずみであり、ひずみは電流と対応関係にあることから、モデルbは、マクスウェルモデルとよく対応できていることがわかります。

モデルdは、入力が定常電圧でした。これは、フォークトモデルの入力が応力であり、応力は電圧と対応関係があることから、モデルdは、フォークトモデルとよく対応できていることがわかります。

では、モデルaとモデルcは、誤っているのでしょうか？

モデルaは、応力との対応関係で、マクスウェルモデルにはない、時間発散時の残留応力が生じています。

モデルcは、ひずみとの対応関係で、フォークトモデルにある、時間発散項の残留ひずみが生じていません。

この問題は、いずれ解決するでしょう。