粘弾性のモデル、マクスウェルモデルとフォークトモデルの統一モデルと相似な電気回路モデルについて
- S Y
- 2023年1月3日
- 読了時間: 2分
更新日:2023年1月4日
0.参考文献
[1]
1.前回の復習
前回、マクスウェルモデルとフォークトモデルの電気モデルを考えました。
電気モデルa~dを考えました。

図1 (a)V=const. (b)I=const.
同様に、RとCが直列に接続されていることを考えます。図2です。

図2 (c) V=const. (d)I=const.
以下の表に、各電気回路とマクスウェルモデルおよびフォークトモデルとの相似関係を示します。




2.図1と図2の両者を統一した電気回路
図3の回路を考えます。

図3 統一回路
入力箇所から反時計回りに、R、C、L、そしてRC並列回路を直列接続させます。こうすれば、キルヒホッフの法則において、電位差を線形和で表すことができます。
3.入力が定常電流である場合
RC並列回路(電圧v_(RC))において、d(q1)/dtはコンデンサ(電圧v_C)の、d(q2)/dtは抵抗(電圧v_R)の電流とします。定常電流ですから、インダクタンスにかかる電位差は0となります。以上を踏まえて、微分方程式は次のようになります。
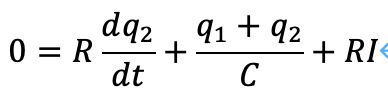
これを解くと、次のようになります。

いつでも、電位差の絶対値は、抵抗とコンデンサで等しいことがわかりました。
抵抗とコンデンサにかかる電流は、次の通りです。

時間を無限大に発散させると、抵抗の2倍だけ、コンデンサに電流が流れていることがわかりました。
4.入力が定常電圧である場合
キルヒホッフの法則から、次の関係式を得ます。
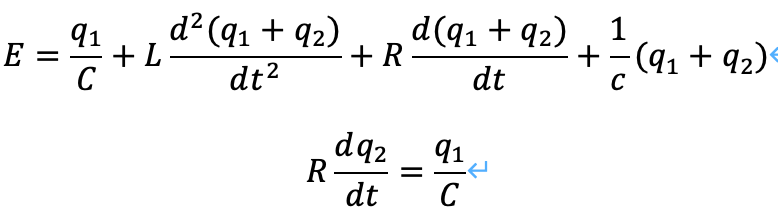
連立方程式から、次の微分方程式に整理できます。
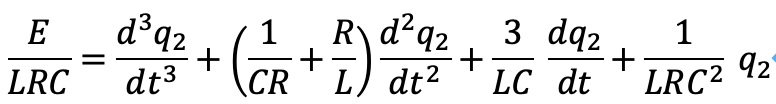
3階微分方程式となることがわかります。
結局、2階微分方程式と同じ原理、斉次解をCexp(λt)として仮定し、3次方程式の問題に帰着します。wolfram alphaにより、3次方程式の解を得ます。(λではなく、xと入力しました。)



また、特解はq2=CEですから、一般解は次のようになります。

ここで、たとえば2重解の場合は次のようになります。

また、3重解の場合は次のようになります。

ところで、それぞれの場合における抵抗に流れる電流は次の通りです。
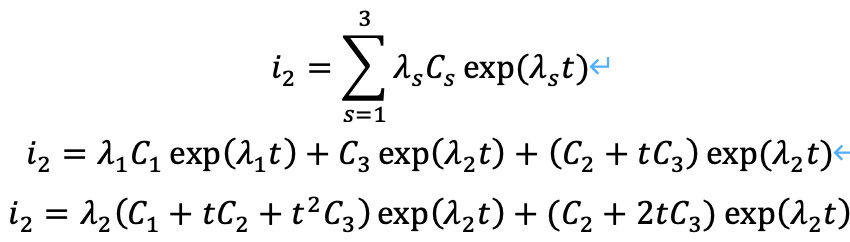
電流から電圧を求め、整理すれば、以下の物性値がわかります。
並列回路の電位差

コンデンサに流れる電流
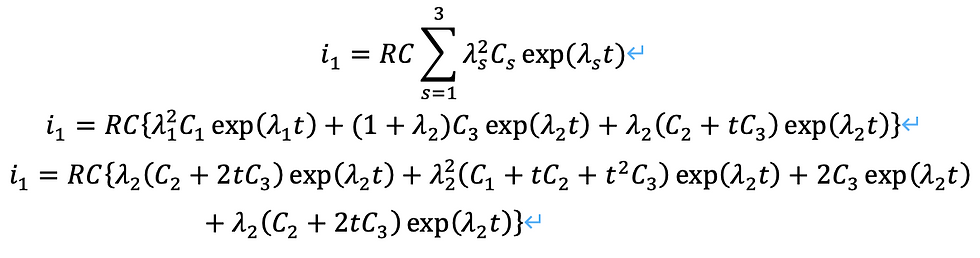
電流の和

抵抗にかかる電位差の合計

インダクタンスにかかる電位差

コンデンサ全体にかかる電圧

5.まとめ
以上が、統一モデルの電圧、電流の解でした。
電圧を応力として、電流をひずみとしても、力学的相似が成り立つため、相似性から解を得たことになります。
これが、粘弾性流体における、マクスウェル=フォークト統一理論です。


コメント