隣接する3つの素数を辺の長さにもつ三角形に共通点はあるか？

[1]かつての私の記した英語の課題

[2]鞍点と曲率について

[3]

[4]アンドリカの予想

[5]

1.復習

隣接する3つのフィボナッチ数は、ユークリッド空間、すなわちガウス曲率が0であるような、あるいは曲率半径が無限大であるような空間においては、これらを辺の長さとする三角形を描くことはできないという問題がありました。そこで、どのような空間なら描けるのかを調べ、結果を得たのが前回の記事[3]でした。

2.復習その2[4][1]

以前、次の予想を立てました。

「任意の隣接する3つの素数により、ユークリッド空間に三角形を描けるだろう。」

これは、アンドリカの予想よりは若干弱い主張ながら、証明するのが難しいものでした。

これが正しいかどうかはわかりません。が、今回はさらに踏み込んだことを考えます。

3.今回考えたいこと

隣接する3つの素数を辺の長さにもつ三角形は、共通点があるか？ということです。

特に、長さではなく、角度の観点から考察していきます。非ユークリッド空間で考察するようになっても、考察しやすいだろうと考えたからです。

4.前提条件

三角形PQRを考えます。

各頂点に対応する長さp,q,rは隣接する奇素数とします(p=2の時は、三角形が成立しません)。

長さがrの辺と、長さがpの辺のなす角をθ1、長さがrの辺と長さがqの辺のなす角をθ2、残りの1つをθ3とします。

この時、明らかに次の関係式が成り立ちます。

5.各θについての正接[5]

三角関数の公式を用いて整理すれば、次の関係性に気づきます。

ここで、記事[5]の関係が成り立つので、次の性質を満たします。(普通に計算しても気づきます)

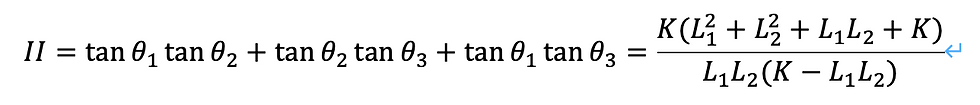
ちなみに、I、II、IIIは、3次テンソルの不変量です。

6.発見

数値実験をしました。

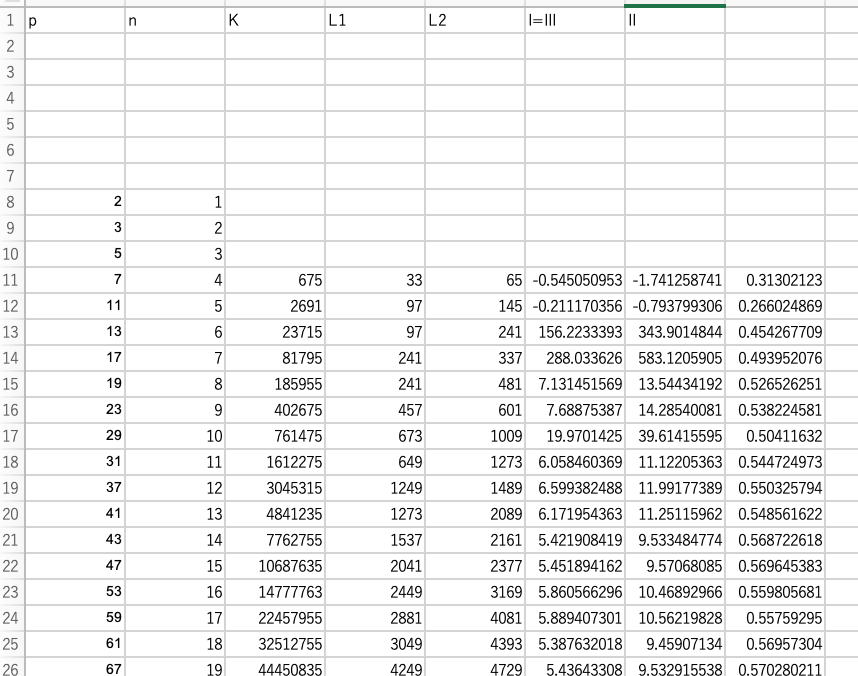
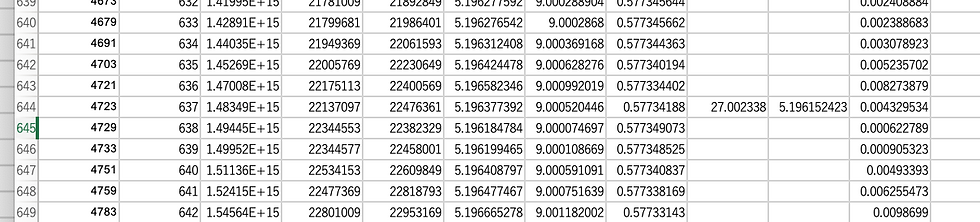
すなわち、

I=III=3*sqrt(3)、II=9となります。

テンソル不変量を用いた固有値方程式は次のとおりです。

元のテンソルは正接についての式だったので、これも正接であるとすれば、θ=π/3[rad]を示していそうなことがわかります。

実部が1/2になるのが不思議ですね。

最新記事