サイクルが数であると捉えた場合、数はどのように表せるか?
- S Y
- 2022年10月12日
- 読了時間: 3分
[1]
[2]
[3]
1.復習

図1 スカラーリンク
サイクルに対して、宇宙際タイヒミュラー理論のθリンクと同等の、スカラーベクトル(黒)を導入しました。定義ではベクトルの性質はない、スカラーの性質を持っています。ところが、繋がっているサイクルの性質のために、ベクトルの性質が生じます。
また、ブラックホールを形成する2体の静止エネルギーを踏まえた、任意の物理現象について、以下の関係が成り立ちます。

以前の記事では、エントロピー行列の相似性を踏まえた上で、数とは何か?を考えました。
また、サイクル論で重要なエントロピー行列について、n乗の性質については、参考文献[3]にまとめました。
2.パスカルの三角形
サイクルを点とみなし、スカラーベクトルによるつながりについて考えます。
図1における左下を起点とした場合、各サイクルへの行き方が何通りあるかをプロットします。

これが明らかにパスカルの三角形であることは容易にわかります。
以上の結果から、サイクルはパスカルの三角形の数であることが推測できます。そこで、次のように考えます。

この時、次の関係式が成り立ちます。
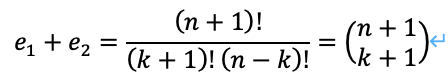

以上から、次のように整理することができます。

3.微分方程式の解釈

τによる微分は、積の結果についてまとめている空間の接平面を与えていることと同じです。これが和の空間に対してαという倍率により一致させることができることを意味しています。
4.微分方程式の解
1章では、スカラーベクトルによるリンクを考えました。2章では、スカラーベクトルによるリンクが、パスカルの三角形の性質と似ていることから、全く同値であると推測しました。3章では、和の空間と積の空間についての解釈を、方程式が与えてくれることを示しました。
このリンクの形について、τに依存しません。n,kを用いた変換は無次元であるからです。αという倍率のみがτの関数であることがわかります。(両辺の次元を踏まえると明らか)。
以上から、次の関係式にあることがわかります。

ところで、定義から次のように考えることができます。
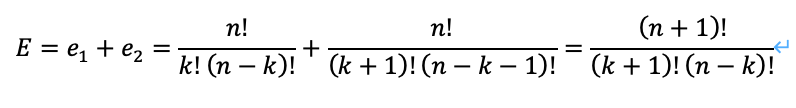
ここに、スターリングの公式を用いて、次のようになります。

これを整理すれば、次のようになります。
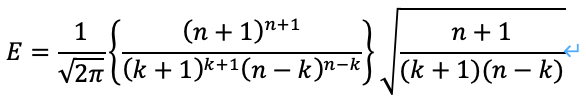
以上から、次のように整理することができます。
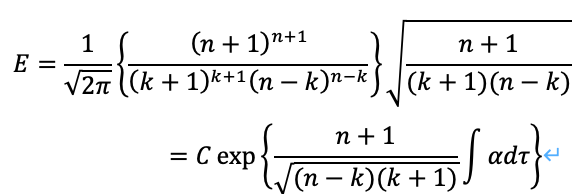
αについて次のように与えることができます。
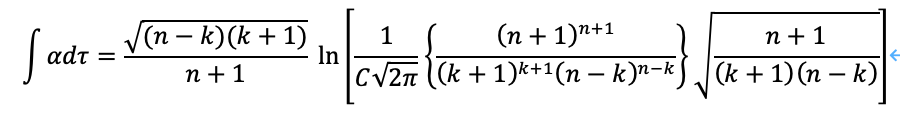
すると、左辺はτで積分されているため、明らかにτの関数になるべきなのにも関わらず、右辺はτの関数とはならないことに気づきます。
また、実はnとkの2変数関数になっていることに気づきます。
以上から、左辺はラプラス変換であることに気づきます。(ある意味で、ラプラス関数は、1変数を2変数に変換する性質を持っている訳です。)
すると、α=f(τ)exp(-sτ)とし、τについて0→∞とすれば、s=n+ikなどと定義することにより、ラプラス変換として考えることができます。
つまり、ラプラス逆変換を考えることで、f(τ)が求まる訳です。
結論
サイクルを数と捉えると、それはパスカルの三角形に現れる数となります。
これをもとにすれば、倍率αについては、ラプラス逆変換により具体的に与えることができることがわかりました。


コメント