(修正版)数とは何か?〜足し算と掛け算の関係式〜
- S Y
- 2022年10月4日
- 読了時間: 3分
0.参考文献
[1]
[2]
1.修正[1]

前回の記事で、この式を整理した結果、以下の式を得られるとしました。

これには誤りがありました。正しくは、以下の通りです。

2.数とは何か?[2]
もし、エネルギーを示すe_1, e_2なる式に対して、実はe_1とe_2が数であるとすれば、次の微分方程式は、相加平均と相乗平均についての、等式を用いた関係式であることがわかります。τは固有時です。

ここに、αは何らかの定数です。
まずは、数空間について、各点にはその固有時間の情報f(r_i)と固有空間の情報が次の関係にあると考えます。ただし固有時間については、微小区間ετを考え、各点についてp_i倍に"引き伸ばされて"いると考えます。特殊相対性理論において、cτを変位と同じ次元で捉えました。これに倣って、ετp_iを考えます。
(数空間は、ある意味でスライム状であると考えています。)

サイクル論[2]において、状態数W(=T)について、次の関係式を考えたことから、自然な発想かと思われます。τは固有時であり、エントロピーと類似した(あるいは、ほとんど同等の)概念でしょうから。

また、Tについてのスケール、あるいは「振幅」が{f(r_i)}^2で意味していると、捉えることもできます。
実際この時、微分方程式の左辺と右辺について、それぞれ次のように解けます。
左辺
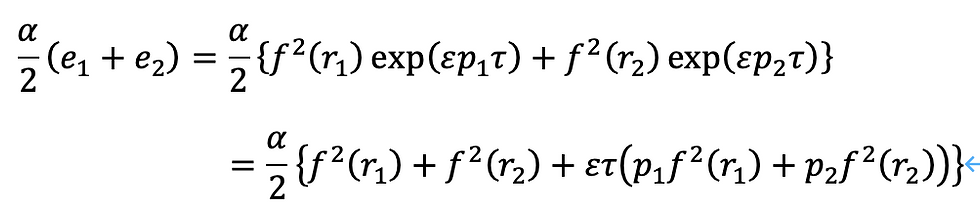
右辺

この結果から2つのことを考察できます。
A 双対数εの係数を比較することで、0乗について次の関係式にあることがわかります。

このことから、f(r_1)とf(r_2)は直交することがわかります。
B αについて、次のように整理することができます。

途中、以下の関係式を用いました。
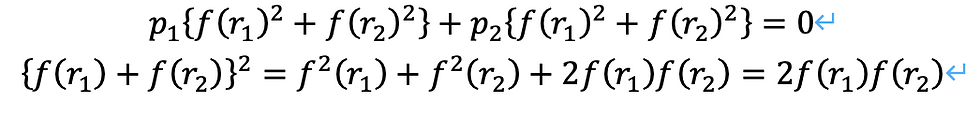
特に、無限遠においては変形がほとんど見られないとしてp=0と、特異点近傍においては(ストローの近く)では変形が最も激しいとしてp=∞として考えると、αの絶対値は等しく、互いに加法の逆元となっていることがわかります。

すなわち、以下の結果を得ます。

次元解析をすれば、確かにαはτ^(-1)の次元を持ちます。
また、仮に無限遠から考えた場合をプラスとすれば、特異点の近傍から考えた場合はマイナスとなります。つまり、符号が変わるのです。
3.対称性
今回の微分方程式とその解について、以下の対称性があることがわかります。
A 並進対称性
無限遠、あるいは特異点の近傍から、任意の空間座標を観察したときに、数の足し算と掛け算の性質を結ぶ倍率αは一定である。(2章で示した通り)
B 回転対称性
2つの数の存在する数空間について、これを回転することを考えます。これでも、微分方程式の形は変わりません。


C 時間と空間の同一性
時間と空間は本質的には同等であるとする対称性のことです。これは、固有時と固有ベクトル(座標)について、同等に扱ったことに起因します。


コメント