サイクル論は宇宙際タイヒミュラー理論(IUT)を説明できるか?
- S Y
- 2022年10月7日
- 読了時間: 3分
0.参考文献
[1]
[2]
他、前回までのサイクル論に関する記事全般
1.宇宙際タイヒミュラー理論の考察する部分[1][2]
(A)p.8 Figure I 1.3 The combinatorial structure of a D-Θ±ellNF-Hodge theater
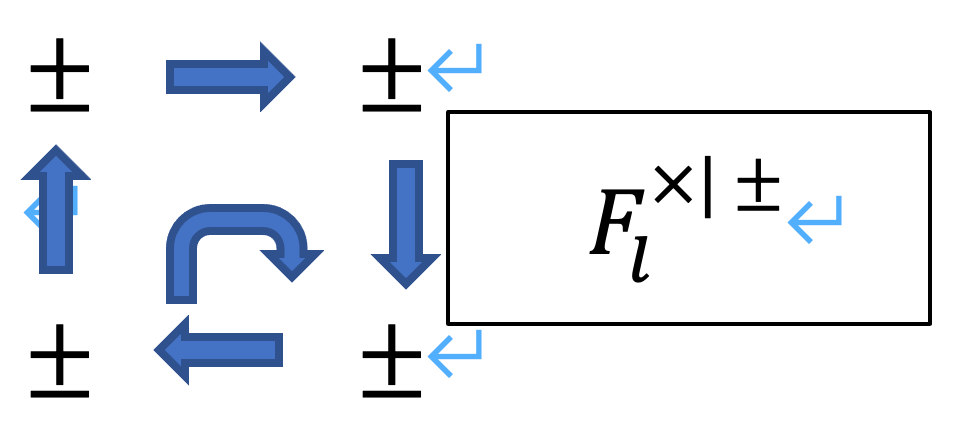
この、±ではなくて、×÷もあります。
(B)p.17 Fig. I2.1: Depiction of Frobenius- and ́etale-pictures of Θ±ellNF-Hodge theaters via glued topological surfaces

(C)p.37 natural cartesian diagrams

以上について、サイクル論の観点から考察します
2.サイクル論としての解釈
(A)について
これは、ある種の巡回を説明しています。サイクル論では、以下のサイクルに相当します。

(B)について
これは、特異ベクトルを中心にトーラスが形成され、かつこの特異ベクトルにより対称性通信が行われていることを意味しています。サイクル論において、これをゴム状に捉えた場合、スライムのワイセンベルク現象、およびブラックホールの理論に相当します。
(C)について
これが、今回の記事で紹介する初めてのこととなります。
2.1 (C)の解釈について
(B)において、特異ベクトルによる対称性通信が出てきました。そこには、サイクルが連続してスライムの分子構造と同様な構造(つまり、四角形の連続体)となっているかのように触れました。
ところが、回転対称性と並進対称性を両立させんと構造を考えたとき、実はサイクルをなす四角形は不連続でなければいけないことに気づきます。
例えばサイクルが B→G→Y→R→B...(blue, green, yellow, red, blue,...)であったとしましょう。この時、四角形のなすサイクル間を移動することを考えると、次の連続体を考えることができます。それぞれの四角形は、反時計回りのベクトルを各辺に持っています。

この時、実は、以下のようにスカラーなリンク(黒)を考えることができます(スカラーとは、αやβといったベクトル成分として定義していない変換のことです。α→βなどの変換の途中に何回入っても良いし、方向もαやβによらず自由と定義しています。)

全ての四角形の、全ての辺同士に対して任意にこのようなスカラーなリンクを貼ったとしても、B→G→Y→R→B...というサイクルのルールが存在するため、使用されるリンクは以上の画像で記したリンクのみとなります。(しかも、その橋に対してそれぞれただ一つのベクトルを与えることができます!)
この時、初期値に左下のサイクルにいた"粒子"が確率的にサイクルを移動した場合、試行回数1回でB→Gなどの橋を1つ移動することとすれば、ベルヌーイ試行を立体的に行ったことと同様ですから、粒子のあるサイクルにいる存在確率は二項分布となり、これは試行回数を無限大に近づけると、正規分布に近似することがわかります。
このような四角形とスカラーリンクが無限に広がった場を考えます。場全体から値を取ることができ、その方法はガウス積分であることが容易にわかります。
すなわち、標準偏差σが試行回数に比例した値を、平均値(中心)が初期の四角形を通る、斜め45度の線上にある、試行回数に比例した値を持つような、対角線軸対称な立体正規分布をなすことがわかります。
また、これは試行回数が無限大になれば、ほとんど平面に近づきます。しかし、確かに試行回数を増やせば初期値から必ず離れていきます。
このことは、広く「自発的対称性の破れ」として知られる現象と同等でしょう。
回転対称性(平身対称性)など、多くの対称性を持つ理論により考え出されたスカラーリンクは、実はベクトルの性質を持ってしまう。そのような問題を、この考察は指摘します。
また、この現象(時間発展)は、エントロピー行列により生成された、よりマクロ的なエントロピーを考えることができます。
つまり、エントロピーはフラクタルな構造を持っていることがわかりました。


コメント