素数空間とサイクル論の話

0.参考文献

[1]

[2]

1.前回の復習

前回の結果から、隣接する4つの素数について、最大と最小、その他2つの2グループに分けた時、それぞれに数非線形空間、sqrt(p1p2)、sqrt(p3p4)を考えることができ、その時間微分空間は線形で、「倍率」αは互いに等しいらしいことがわかりました。

2.前回の考察

素数非線形空間の倍率αを、別の素数非線形空間の倍率α'へ変換する、倍率βを考えました。

そもそも、ここでいう「倍率」とはなんだったのでしょうか？

あくまで予想ですが、数空間が以上で論じたように物理空間に属するのなら、力学の理論で使用される、ラグランジュの未定乗数のことであると推測されます。

実際、非線形空間の形状を決定する関数(拘束条件?)が時間の2次関数であるらしいことがわかりますし(?)、(時間の1回微分の空間にて、線形となったため)。拘束力についての式と捉えることもできます。そのため、未定乗数を用いることにより運動を表現できるとも考えられます。

3.βが1に近い値を持った意味

βが1に近い値であるということは、αがほとんど同じ値をとっているということです。ですから、数空間のサイズがどの素数に対してもほとんど同じであることが推測できます。

4.αの添字についての考察

方程式にて、α(n,n+3)、α(n+1,n+2)は互いに近い値をとり、α(n+1,n+4)、α(n+2,n+3)は互いに近い値をとり、α(n+2, n+5)、α(n+3, n+4)は互いに近い値をとり…と、n+mについて、mの組み合わせに注目します。

すると、α(n+m1, n+m2)、m1<m2とした時、m1=m2+3か、m1=m2+1かのいずれかのモードとなり、それぞれ交互に現れることに気づきます。

この添字について整理すれば、以下の関係になることに気づきます。

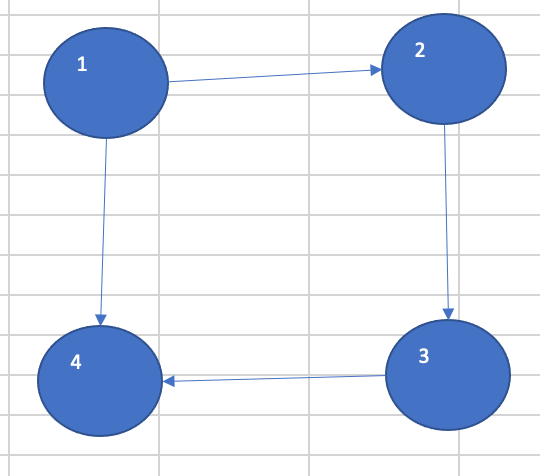
これは、サイクル論の、特にスカラーリンクについての関係性に同じになっていることに気づきます。

また、サイクル論によれば、各頂点に対してサイクルが生じていることが知られていますので、添字それ自体は、何らかのサイクルが存在することが推測できます。

その添字によるサイクルこそ、数空間を構成する2つの素数のうち一方の正体であると考えることができるでしょう。

最新記事