フィボナッチ数列の性質一覧(備忘録)
- Yume Isioto
- 2022年1月2日
- 読了時間: 3分
更新日:2022年1月11日
今回は、フィボナッチ数列の性質とその証明・予想を紹介していきます。
目次
1)三項間漸化式(定義)
2)一般項[1]
3)ゼッケンドルフの定理
4)ゼッケンドルフの定理(減法[石音夢])[2]
5)自然数の無限級数表現[石音夢][3]
6)多項間漸化式その1[4]
7)多項間漸化式その2
8)多項間漸化式その3
9)二項間漸化式
10)積の公式
11)積の公式2
12)自然数倍の公式
13)フィボナッチ数の逆数の無限和
14)一般化ゼッケンドルフの定理
参考文献
[1] https://manabitimes.jp/math/643 高校数学の美しい物語「フィボナッチ数列の一般項と数学的帰納法」
[3]
[4]
https://examist.jp/mathematics/recurrence-formula/fibonacci/ 受験の月 フィボナッチ数列の漸化式、有名性質とその証明
1)三項間漸化式(定義)
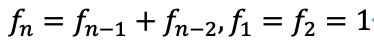
初項と第2項が1であると定めることで、それ以降のフィボナッチ数が定まります。またこの数式は定義式なので、証明はありません。
2)一般項[1]
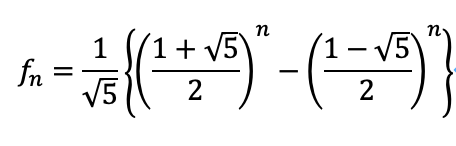
ビネの公式と呼ばれるものです。特性方程式の解をうまく使います。
3)ゼッケンドルフの定理(加法)
任意の自然数は連続しないフィボナッチ数を用いて一意に和の形で表せる。
例:73=55+13+5
これは帰納法で証明できます。
4)ゼッケンドルフの定理(減法[石音夢])[2]
任意の自然数は連続しない、フィボナッチ数から1を引いた数の差で一意に表せる。
例:73=89-(21-5)
これも帰納法で証明できます。おそらく、ゼッケンドルフの定理(加法)と同値なはずです。
5)自然数の無限級数表現[石音夢][3]
任意の自然数は連続しない、フィボナッチ数から1or2を引いた数の逆数を用いて、一意に表せる。
ゼッケンドルフの定理(減法)から導かれます。
6)多項間漸化式その1[4]
以下の式は良く知られたものです。
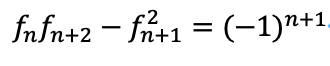
どうやら、数学的帰納法をうまく使うことで、この式から1)の式を導けるそうです。
7)多項間漸化式その2[石音夢]
6)の式をより一般化させます。

ここで、n>=mであることに注意してください。(等号成立の時、両辺は0になります。)おそらく、数学的帰納法で同様に証明できるはずです。
8)多項間漸化式その3[石音夢]
フィボナッチ数を中心に、対称な距離にある2つのフィボナッチ数は次の関係式を満たすようです。7)の式においてmを2mに変えた場合と併せて使うことで、面白そうな結果が得られそうです。

9)二項間漸化式[石音夢]
フィボナッチ数は以下の関係式を満たします。
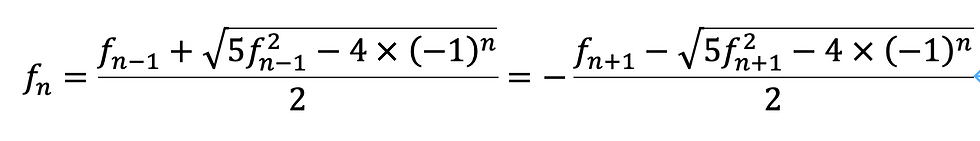
6)の式にf_(n+1)=f_(n+2)-f_(n)を代入します。整理して二次方程式を解くことでf_nとf_(n-2)の関係式を導けます。うまく整理することでf_nとf_(n-1)の関係式を与えられます。
10)積の公式[石音夢]
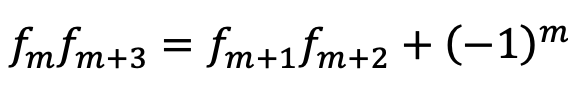
連続するフィボナッチ数4つについて、最大と最小をかけたものと、他2つをかけたものについての等式です。まだ証明はしてません。ですから、数値実験によって得られた予想です。
11)積の公式2[石音夢]

隣り合う2つのフィボナッチ数に関するもう一つの予想です。
12)自然数倍の公式[石音夢]
m>=tとした時、以下の結果を得られます。kは自然数です。

つまり、f_m-f_(m-t)f_(t-1)は、f_tの自然数倍にいつでもなるという予想です。また、kはおそらく奇数番目のフィボナッチ数となるだろうと推測しています。
13)フィボナッチ素数
フィボナッチ素数は無数に存在します。

a:奇数、b:偶数とします。(a>b)
この時、

となります。ここで、f_a, f_bが共に奇数であると仮定すれば、この式はf_a, f_bが原子ピタゴラス数となりえます。その必要条件は、

を満たす自然数m,nが存在することです。ここで鳩の巣箱原理より、フィボナッチ数列から等間隔に数を3つ選択した場合、すべて奇数、あるいはすべて偶数となることはないので、f_(a-b)とf_(a+b)のいずれかは偶数となります。そのため、この式は成り立つだろうことが推測できます。
ここで、ピタゴラス素数が無数に存在することから、フィボナッチ素数も無数に存在するだろうことがわかります。
13)フィボナッチ数の逆数の無限和
以下の式が成り立つ

14)一般化ゼッケンドルフの定理
次の漸化式で得られる数列について。

任意の自然数は、N個までの、これらの数列の要素の和で一意に表せる。ただし、(N-2)個までなら隣接しても良い。またNは2以上とする。減法により、任意の自然数を同様にして一意に表せる。


コメント