ピタゴラスの定理についての考察
- S Y
- 2022年10月4日
- 読了時間: 2分
0.参考文献
[1]
[2]
[3]
1.ピタゴラスの定理とは、自然数に対して次の関係が存在することがわかります。[1][3]

つまり、次の関係式が正しいということとなります。

εの次数ごとに係数を比べます。
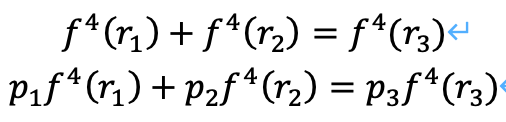
以上から、次のようになります。

両辺を比較すれば、p_2=0であることがわかります。
ところで、p_2=0とは、[1]で以前説明した通り、スライム状の数空間に対して、特異ベクトルから無限遠の位置における性質のことでした。すなわち、スライムの変形がほとんどない地点というわけですから、これはユークリッド空間を考えていることがわかります。
また、この結果から、以下の式が成り立つことがわかります。

これを整理します。ただし、以下の式を使います。

整理すれば、次のようになります。

以上から、数e_1, e_2, e_3について、スライム空間は以下のように分布していることがわかります。
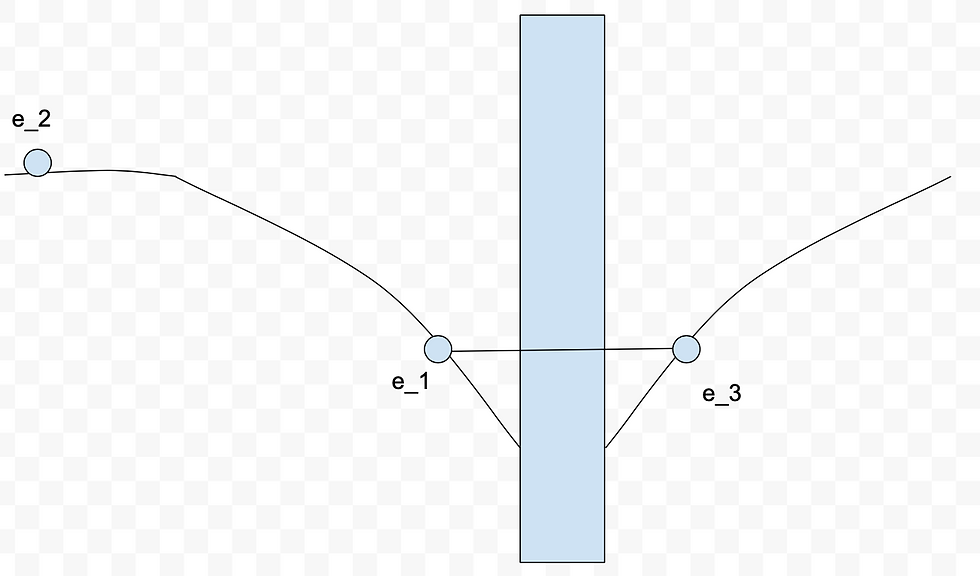
ここに真ん中の棒は特異ベクトルを意味しています。この特異ベクトルから同じ距離に、e_1とe_3がある(同じαを持つ)ことがわかります。
また、e_2は、特異ベクトルの位置から無限遠の位置にあることもわかります。
ところで、[3]によると、特異ベクトルの周囲には、トルクに依存した玉が特異ベクトルの周りに連続的にできます。つまり、連続的な性質を持つ数、すなわち0より大きな実数を長さにもつ三角形が存在することがわかります。
この球の山谷について、その離散性を捉えることにより、自然数でも同じような状況が存在しうることがわかります。
また、このベクトルで不変であるe_2が無限遠の位置にあることは、そのままユークリッド空間であると捉えられます。
だから、ピタゴラスの定理が成立することを証明できました。


コメント