ハッブル定数は、石音角速度か？そうだと仮定した場合、インフレーションやビッグバンに相当するブラックホールの形成で使用された「星」の物性値はいくらか？

0.参考文献

[1]

[2]

[3]

1.復習

石音角速度は、次のようになります。

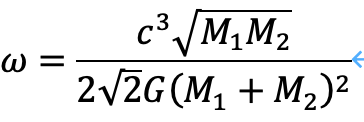
2.参考文献

ハッブル=ルメートルの法則によれば、天体がある地点から遠ざかる速さ(後退速度)は、ある地点から天体までの距離をDとすれば、次の関係式が得られます。

3.スライムの、ワイセンベルク現象について

スライムに棒を刺して、この棒を中軸を回転軸として回転した時、スライムは上昇する現象が起こります。これをワイセンベルク現象と呼びます。

この時、棒からの距離に対して粘性による遅れについて考えると、棒からの距離に比例して遅れることがわかります。

するとこの遅れこそ、ハッブルが「宇宙は膨張している」と判断した現象の所以であるとも、考えることができます。

つまり、ハッブル=ルメートルの法則の帰結が、宇宙の膨張ではなく、単にスライムのワイセンベルク現象における、空間に違いによる遅れであるとすれば、膨張しつつ、時間的に周期的な宇宙を考えることができることがわかります。

4.石音角速度がハッブル定数と等しいとき、宇宙を形成した2体の星の質量はいくらか？

3章で提唱したことを一言で言えば、次のようになります。

「宇宙の誕生はブラックホールで説明でき、かつブラックホールがワイセンベルク現象で説明できるのなら、ハッブル定数は、石音角速度と等しいのではないだろうか？」

そこで、実際に計算すれば、宇宙を形成したブラックホールを成した2つの「星」1組について、それぞれの質量比を求めることができます。さらに、そのブラックホールのシュワルツシルト半径もわかります。

これをM_2について解くと、次のように計算できます。

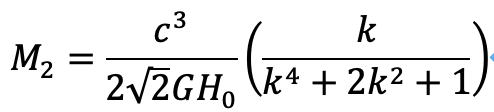
ここにこの時、シュワルツシルト半径は次のようにもとまります。

まずは、ブラックホールの質量について次のようにもとまります。

これより、シュワルツシルト半径は次のようにもとまります。

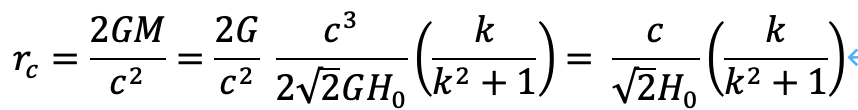
ここで、速度について考えます。

5.kの制限について

物理的には、光速を超えて運動すると、空間が歪んでしまいます。すなわち、スライムにおける「しわ」が生じてしまうのです。

ところで、スライムのワイセンベルク現象において、ねじれないのは、棒に接した部分か、無限遠ですから、接した部分(シュワルツシルト半径)の速度が光速であれば良いわけです。

すると、次の関係式が得られます。

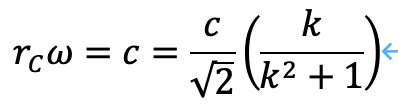
すると、kが定まります。

以上の結果から示されることは、ブラックホールを形成する2つの星の質量比が一つに定まってしまうという矛盾です。

このことは、ブラックホールができる前から、どの星がブラックホールを作るのかが決まっていたかのような結果となります。

また、質量比が複素数値をとるということは、質量も実は複素数値を持つということがわかります。

最新記事