エルデス・シュトラウスの予想に対する考察(Part3)
- S Y
- 2021年10月13日
- 読了時間: 2分
0.参考文献
エルデスシュトラウスの予想1(場合分け法) - 中高生にもわかりやすい数学
1.前回の復習
前回までの考察により、4s-1型、6s-1型の素数とそれらの倍数についてはエルデス・シュトラウスの予想が正しいことを示せました。また、5(12t-5)などの特別な場合に関しては、同様に予想の正しさを示すことができることがわかりました。
2.今回考えたいこと・結論
一度、エルデス。シュトラウスの予想から離れて、24s+1型の自然数μについて、4/μを、分子が1である分数と別の自然数τ、αを用いて表せるかを考えたいと思います。
最終ゴールは以下の式が成立することです。
24s+1型自然数μに対し、5μ=4τ+1、μ=3α+1を満たすτ、αが存在して、以下の等式を満たします。

(式2.1)
3. μ=24s+1において、4/μと等しい値もろもろ
以下のように変形してみました。
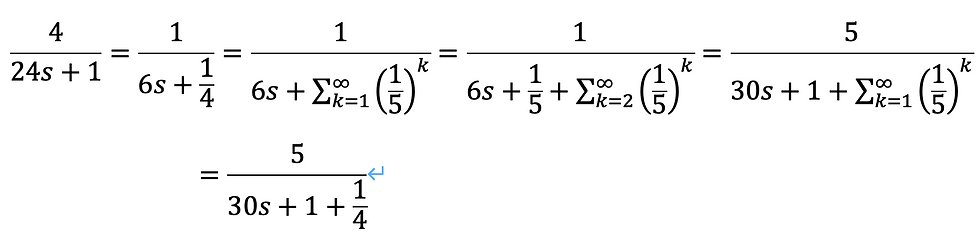
(式3.1)さて、30s+1=(24s+1)tとなる自然数s,tは存在しません。そのため、30s+1型の自然数τを用いて次のように変形することができます。

(式3.2)第二辺と最右辺について整理すると、以下のようになります。

ここで、τ=30s+1ですから、エルデス予想によれば、自然数a,b,cが存在して次の式を満たします。

(式3.3)式3.2に代入すれば、以下の式が成立します。

4. α=8sにおいて、4/μと等しい値もろもろ
α=8sより、3α+1=24s+1=μとなります。

(式4.1)両辺をそれぞれαμで割って、

(式4.2)となります。
5.まとめ
式3.3と式4.2について、うまくまとめることができ、式2.1のように表せます。


コメント