エルデス・シュトラウスの予想に対する考察(Part2)

1. 前回の復習

n=2,3,あるいは6s-1型素数とそれらの倍数、または6s+1型素数の偶数倍であるとき、エルデス・シュトラウスの予想を一般化した予想が正しいことを証明しました。

2. 今回考えること＆説明

6s+1型の素数nについて、sの偶奇を考えます。

s=2t, 2t-1(t>=1)であるとき、それぞれ6s+1=12t+1, 12t-5となります。

まずは、12t-5について考えます。

前回考えた以下の式に、a=bu, b=5として計算すれば、a=4tであることがわかります。

以上から、

となります。整理すれば、以下の式を得られます。

続いて、12t+1ですが、再び、今度はtについて、その偶奇を考えます。

t=2g, 2g-1(g>=1)であるとき、それぞれ12t+1=24g+1, 24g-11となります。

まずは、24g-11について同様に考えます。

同様にすると、a=bu, b=11として計算すれば、a=8tであることがわかります。

以下の式が成り立ちます。

整理すれば、以下の式を得られます。

3. 2についての考察

うまくsを2tに置き換えたことで、bを6s-1型の奇数(素数)にすることができました。これにより、例えば4/35などが複数通りの表し方があることがわかります。

また、

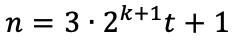
の場合について、同様に考えることができます。すると、以下の関係式を満たすことがわかります。

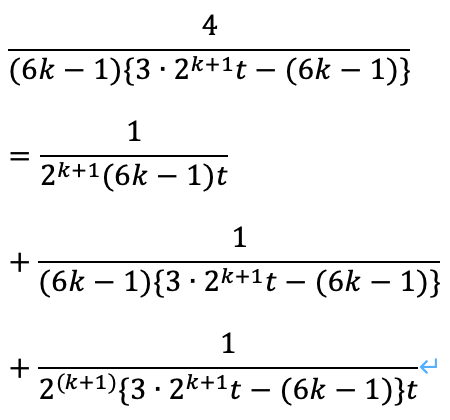
ここで再び、nが6t+1型素数(6s+1型素数と同義)であるとします。そのため、k=0です。代入すれば、以下の関係式を得られます。

続く。

4. 本日のオリンピック

女子サッカー

惜しくもスウェーデンに敗れてしまいましたね。非常に難しいことは承知ですが、決定的なシーンで確実に決め切れていたら、勝っていたかもしれません…。4-3で勝って欲しかったですね。

男子テニス

まさかのジョコビッチ敗退…。ショックです。

ハンドボール男子

接戦を競り負けてしまったようで、残念ですね。

バドミントン混合ダブルス

銅メダル、おめでとうございます！

フェンシング

金メダル獲得おめでとうございます！

柔道

金メダル獲得、おめでとうございます！