改造版リーマン多様体の提唱とリーマン予想に関する考察1
- S Y
- 2022年4月4日
- 読了時間: 3分
0. 参考文献
[2]https://ja.wikipedia.org/wiki/バーゼル問題
[4]https://jp.mathworks.com/discovery/fourier-transform.html
1.リーマン球面[1]
一般的に知られるリーマン球面は、直交3軸空間の原点を中心とする、半径1の球に相当し、うち2変数軸はそれぞれ実軸と虚軸に相当します。この(0,0,1)と、ある複素数の点(a,b,0)を通る直線に対して球面との交点はただ一つ存在します。こうして複素平面と球面を1対1対応させることができるのです。詳しくはwikipediaをご覧下さい。
2.新リーマン球面
新しいリーマン球面を定義します。直交3軸空間の(0,0,1)を中心とする、半径1の球として定義します。この時、平面(a,b,0)は複素平面に相当し、かつ(0,0,0)で複素平面と新リーマン球面は接します。また、ある複素数の点(a,b,0)を通る球の接線を考えると球面と接線の接点はただ一つ存在します。こうして複素平面と新リーマン球面を1対1対応させることができます。

複素平面(x_1,y_1,0)と新リーマン球面(x_0,y_0,z_0)は以上の関係になります。球の接平面の方程式と、(y_1)/(x_1)=(y_0)/(x_0)を用いて方程式を解くことで、この解を得ます。
3.リーマントーラス面
新リーマン球の考え方を、球ではなくトーラスに置き換えて考えることにします。ここでトーラスの中心はある関数の唯一の特異点であるとします。この時、特異点を除く全ての複素数(a,b,0)とトーラス面(x,y,z)は、接線を用いて1対1対応をします。さらに特異点近傍に対しては複素平面内に描けない程度に小さな空間を改めて考え、そこに対しても1対1対応をさせることができます。
トーラスの定義
・中心を特異点とする
・大半径を双対数εとする
・小半径を1とする
・2変数はそれぞれ実軸と虚軸に対応する
トーラスの性質
・ある関数における唯一の特異点の情報を有している
・任意の関数について、零点とトーラスの対応関係は、複素平面とトーラスの対応と同じ関係にある(関数を通して不変)
バーゼル問題で、オイラーがsin(x)/xに対して零点に関する因数分解を与えた[2]ように、全ての複素関数に対して次のように一意に変換することができます。

ただし、α_kは全ての特異点を、β_lは全ての零点をそれぞれ示しています。一つの特異点はトーラスの中心座標を意味していて、特に特異点が一つだけである関数に対してリーマントーラス面を考えることができるのです。
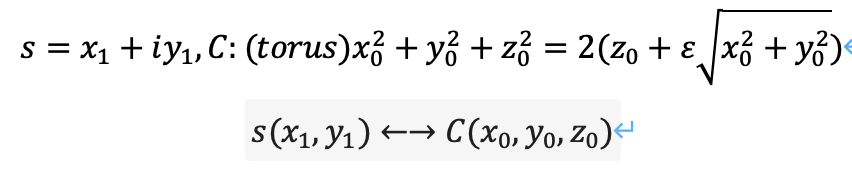
4.メビウスの輪式リーマントーラス面
メビウスの輪は、半周ねじれているために中線で切断すればある1点で接続された2つの輪に分かれます。同じ性質を持つリーマントーラス面を考えると、周期性を持つ関数と対応関係を与えることができます。(周期1つ分とトーラスひとつ分が対応関係)。ただし、周期的に、無限個の特異点が発生するような関数に対してのみ、このような対応関係を与えることができます。
実は、以前の記事で三角関数を、周期的に、無限個の特異点が発生するような関数として無限級数の形で与えることが可能なことを説明しました。[3]
それが、次の式です。

ところでフーリエ変換により、任意の周期関数は三角関数の無限級数で一意に表せます。[4]ですから、任意の周期関数は以上のような形で、周期的に、無限個の特異点が発生するような関数として無限級数の形で与えることが可能なのです。つまり、次の定理を得ます。
定理4.1
任意の周期関数はメビウスの輪式リーマントーラス面に一意に変換可能である。
5. ゼータ関数とリーマントーラス面
ゼータ関数の特異点はs=1のみなので、リーマントーラス面に変換可能です。
トーラスは次のように表せます。ただし、複素数s=x+iyとします。
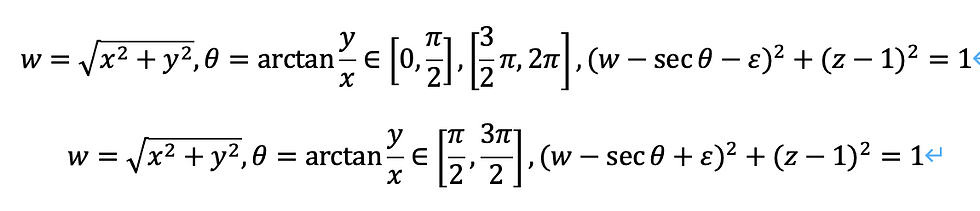
また、球座標系を考えるとき、次の2つの角度がポイントになるでしょう。
ここで(x,y)は複素平面上の点を、z_0は接点のz座標を表しています。

次回は、自明な零点と非自明な零点に対して2つの角度がどのような関係にあるのかを調べます。


コメント