実球と虚球、分離球と接続球の関係性について

0.参考文献

[1]

https://isiotoyume.wixsite.com/website/post/実球、虚球、分離球、接続球の数理、及びスライムの分離モデル

1.実球と虚球、分離球と接続球のパラメータ表示および、方程式

前回の記事にて、実球と虚球、分離球と接続球のパラメータ表示および、方程式を考えました。

上から、実球、分離球、接続球、虚球です。

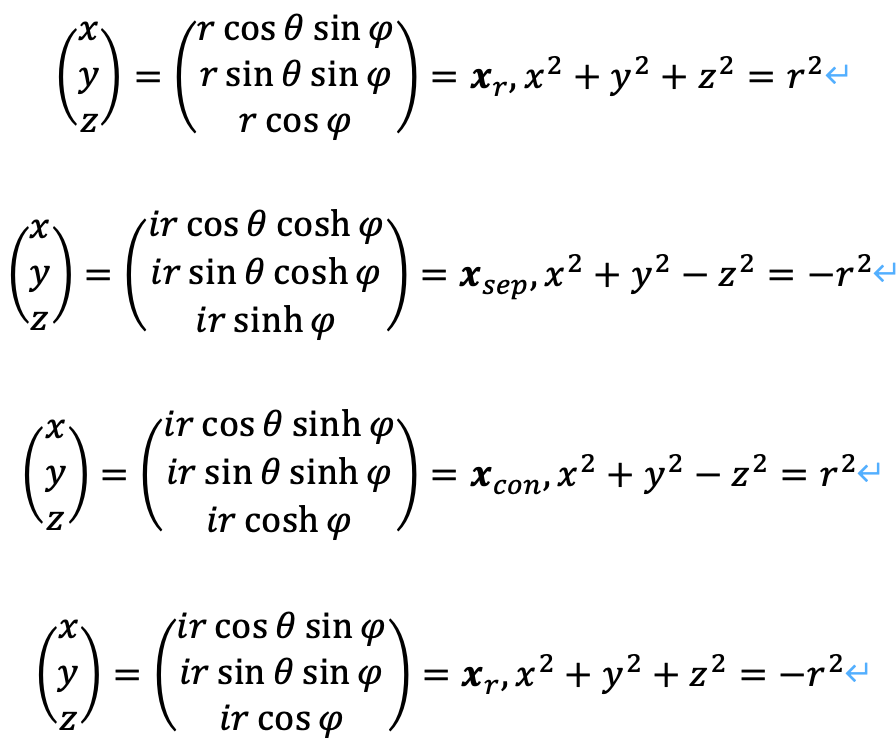
もっとも、パラメータ表示の方法は前回の記事で示したとおり、実球と虚球については複数通り存在することがわかります。

また、分離球と接続球については、実球と虚球と比較してパラメータ表示の方法が少ないです。上に挙げたものと、もう一つずつあります、

2.パラメータの関係について

実球は(r, θ, φ)です。このパラメータについて、rをirに変更すれば、虚球(ir、θ、φ)となります。

φをiφに変更すれば、それぞれ(r, θ、iφ)、(ir、θ、iφ)となります。

接続球のx、yはパラメータ(r, θ、iφ)を用いて、zはパラメータ(ir、θ、iφ)を用いた実球と捉えることができます。

また、接続球から分離球への変換は、前回の記事で示したとおり、φによる1階微分、あるいは1階積分により可能です。

ところで、x、yはパラメータ(ir、θ、iφ)を用いて、zはパラメータ(r, θ、iφ)を用いた実球と捉えた場合は、次のようになります。

分離球です。これをφで微分すれば、接続球となります。