実球、虚球、分離球、接続球の数理、及びスライムの分離モデル

0.参考文献

[1]

高松吉郎著、「微分幾何」、昭和51年9月25日第1版印刷

[2]

https://www.se.fukuoka-u.ac.jp/iwayama/teach/fractional_calculus/tsuuron_fractional_deriv.pdf

1.実球のパラメータ表示

次のようにパラメータ表示をすれば、同じ実球を与えることができます。

(訂正) 右上はsinでなくてsinh です

これは、θとφについて、いずれか、あるいは両方をiθとiφと変更しても、球となることがわかります。

2.虚球のパラメータ表示

次のようにパラメータ表示をすれば、同じ虚球を与えることができます。

これは、rとθ、φについて、rをirにした場合、irかつiθ、φ、irかつθ、iφを考えました。

3.分離球

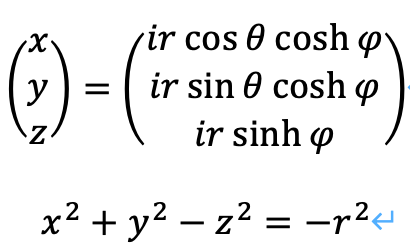
これは、r、θ、φの全てに対して、虚数単位をかけたir、iθ、iφを考えても、それらの組み合わせで作れないパラメータとなります。

4.接続球

これも、r、θ、φの全てに対して、虚数単位をかけたir、iθ、iφを考えても、それらの組み合わせで作れないパラメータを考えました。ところで、z軸からの角度とするか、xy平面からの角度とするかで、分離球と接続球との違いが生じます。

5.球の形状

Geogebraを用いることで、球を描画できました。

青は一般的に知られている実球です。黄色は分離球と呼びました。赤色は、xy平面を通るので接続球と呼びました。白色は、実数空間では描画できませんでした。

6.物理現象としての解釈[2]

実球は、スライムと考えます。

接続球は、スライムの体積を半分にする、分離直前の状態と考えられます。

分離球は、スライムの体積を半分にする、分離直後の状態と考えられます。

ところで、接続球から分離球への関係は、φの1階積分により結びつけることができます。

すなわち、φの分数階積分により、その階数を無次元時刻と対応付けさせることで、連続的な変形を説明することができます。

ここで、Riemann-Liouville微分を考えます。

これは、λ階微分であり、λは有理数と考えられます。

これを用いて、指数関数に対して、次のように求まります。

以上から、coshφについて、次のように求まります。

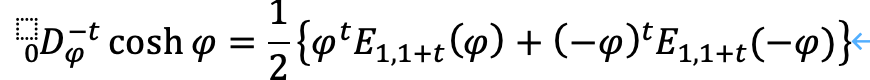
ただし、Mittag-Leffler関数を用いました。

これにより、分数の範囲で連続的な、分離の時間変化を説明する数理を与えることができます。

7.全曲率、平均曲率[1]

実球、虚球、分離球、接続球の全曲率、及び平均曲率は次のようになります。

絶対値を考えると、全曲率と平均曲率が常に一定であることがわかります。

ただし、それぞれの定義式は次のとおりです。

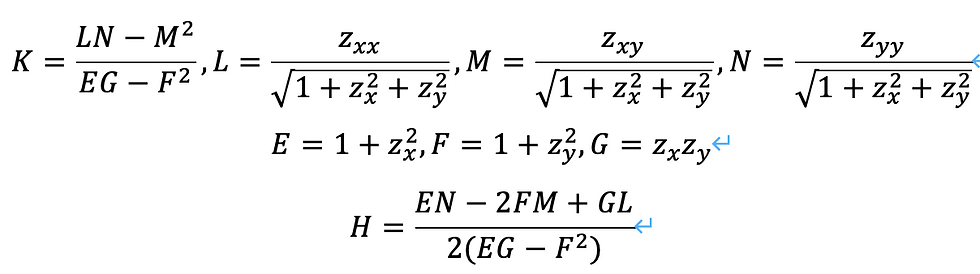
全曲率と平均曲率の絶対値が常に一定であれば、その空間に立っている観測者は、絶対値によってのみ、「自分の空間」についての量を計測できないため、実球、虚球、分離球、接続球のどれに自分が存在しているのかを、定めることができなくなります。ということは、分数階微分により、階数を時間変化量と捉えても、その階数を記録しないと、変換したことに観測者は気付けないのです。

8.スライムの分離についての数理モデル

スライムの分離が始まる直前の状態を接続球でモデル化します。

次に、スライムの分離が終わった直後の状態を分離球でモデル化します。

この間、t*[sec]かかったとします。

u=[0,t*](sec)を考えると、これを無次元化して、u/t*=tとした無次元時刻を考えます。

この時刻tについての時間推移を考えると、次のように求めることができます。