一般のN次双対空間における石音の公式についての考察及びエントロピーについての考察
- S Y
- 2022年8月31日
- 読了時間: 3分
更新日:2024年7月23日
なし(強いて言えば、今までの記事)
1.一般のN次元における石音の公式
以下の等式が成り立ちます。A, B, εはN次正方行列です。
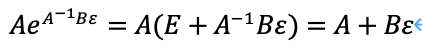
この公式において重要なのは、Bεには逆行列が存在しないこと、及びAには逆行列が存在することです。
2. 一般N次元におけるエントロピー行列の定義
エントロピーSについて、同じ次元の双対空間、及び実空間(a_lmにおいて、l=mのこと)のみが0でない行列を考えます。3次の正方行列においては、以下のように定義できます。

Σ及びΣ_tが正則である必要があります。すなわち、Sには直接現れないc及びdについて重要なのは、それが0ではないということです。また、他の数a,b,e,fにおいても、これが0でないことが重要です。
3. エントロピーの定義から、温度行列を再考する。

ボルツマンにより、エントロピーと温度(状態量を示す変数)は上の関係にあることがわかっています。
これを、2章で再定義したΣを、1章の公式を用いることで考えます。

右辺を単位行列に変換するために、次の2通りの計算方法を考えることができます。Tを中心に両側から計算する方法と、片方から(結局どちらでも同様な結論を得られますが、今回は左から)計算する方法です。

お気づきでしょうか?

このようにすれば、見やすいと思います。αβ=βα=E^(-1)=E、を意味しているわけです。
この結果から、温度行列とは、「エントロピー行列の基本成分と転置成分が互いに乗算の上で可逆になるための橋渡し」であることがわかります。
4.考察
ボルツマンによるエントロピーと温度の定義から、エントロピー行列Sと温度行列Tについて考察しました。
エントロピーはその不可逆性と増大則(断熱系)から、双対空間をうまく使うことにより説明できることがわかりました。
温度行列は、その「温度」が物理的にどのような意味を持つかは不明ですが、固有ベクトルを使うことにより計算することができました。また、そこで現れたcosh関数及びsinh関数は、以前書いた乱流に関する、テニスラケットの原理を用いた考察と関連してそうであることを推測しました。
さらに、エントロピー行列SについてΣとΣ_tに、転置か否かという視点からわけました。石音の定理(exp(ε)=1+ε)が一般の行列に対しても成り立つことを確認しました。その上で、温度行列に対する作用素αと、転置成分からなる類似した作用素βを考えることにより、両者が互いの逆行列となっていることを示しました。
このことから、作用素αとβを用いたある種の「時間反転対称性」を、ある意味でエントロピーの性質として説明できると思います。
注意
E+ε, E+(t^)εの議論について訂正


コメント