パスカルの三角形に対するある性質の証明

0.参考文献

[1]

https://isiotoyume.wixsite.com/website/post/黄金比を無限級数で求める

1.パスカルの三角形のある性質

パスカルの三角形について、次の性質が成立することを、今回、調べたいと思います。

修正)左辺のxは上から、 x^1, x^2, x^3, x^4, ...の誤りです。

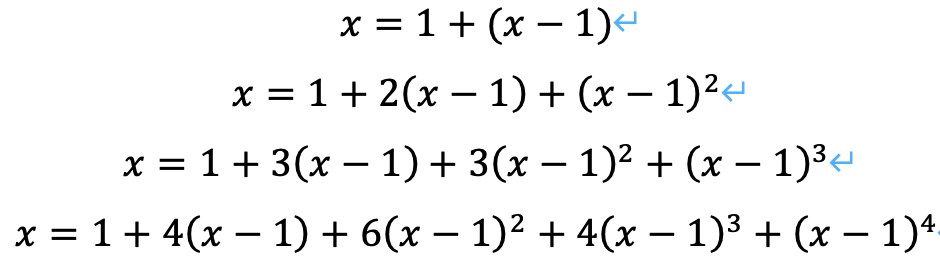
2.ある関数のテイラー展開

次の関数を考えます。

テイラー展開を考えるため、何回か微分します。

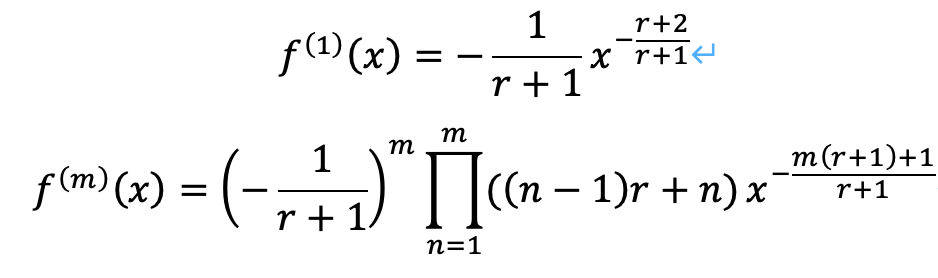
以上から、テイラー展開は次のように与えることができます。

3.p=-1/(r+1)の場合

2章で考えた関数に対し、実数pを用いてp=-1/(r+1)として再度考えます。

一般性を保証するために、x/x_0=yとして、yについて整理します。

注意　0階微分は、もとの数式です。

4.結論

3章で得られた結果を実際に展開すれば、1章の結果を得ます。

5.おまけ

実は、今まで回りくどい考え方で証明しましたが、数行で証明できることに気づきます。

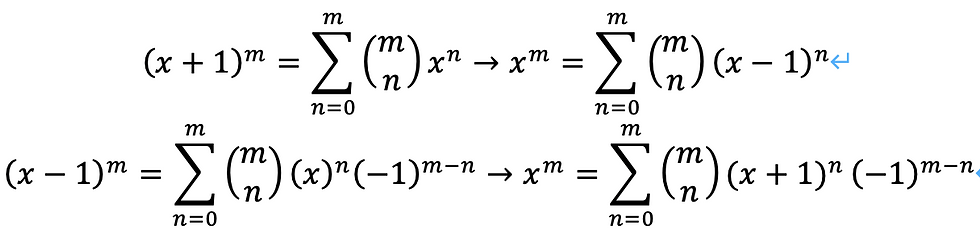
今回の記事の本質は、テイラー展開の新しい景色を紹介することでしたので、ご了承ください。