f(x)=-x^(n+1)+1+x+x^2+x^3+...+x^nの零点についての考察 その3
- S Y
- 2023年2月6日
- 読了時間: 1分
0.参考文献
[1]
1.F(x)の、非実数解の特徴について
前回、次の無限積を考えました。
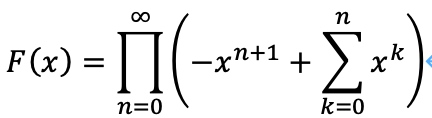
この零点は、任意のnに対して、(n+1)ボナッチ数列の一般項を与えたり、その逆数については、(n+1)ボナッチ数列を係数とする無限多項積を与えるテイラー展開を作ります。
今までは、主に実数解に対して考察してきました。今回は、虚部が0でない複素数解について考えます。
2.部分積の計算値
n>=3でのみ複素数解が出てきませんから、3以上から計算値を考えます。
ただし、一部は実軸対称な解が出てきますから、その場合は偏角が正である解のみ求めます。
計算値は次のとおりです。

以上から(r,θ)に対し、複素数z=(x,y)平面へ変換した上で、次のようにプロットできます。

これらの零点は、素数の性質を握るゼータ関数とは異なり、直線などの規則性はないように見受けられます。


コメント