f(x)=-x^(n+1)+1+x+x^2+x^3+...+x^nの零点についての考察 その1

1.問題

関数f(x)を次のように考えます。

この零点を満足するxの実数解は、(n+1)ボナッチ数列の一般項で使われます。

では、この零点はどのような関数で表せるのでしょうか？

2.数値実験

2.1 推測A

実際に、計算してみました。2列目は式を見て、おそらく次の形になると考えました。

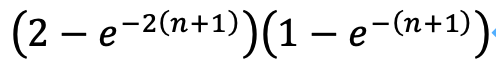
この式で私が推測したことは、目的値2に、指数関数的に近づいていくことでした。

ところが、値が必ずしも一致するわけではないということが、実際にわかります。

2.2 推測B

次の関数となることを仮定します。

この1階及び2階微分を考えます。差分を考えると、次のようになります。

ところで、g(m)の定義から、1階微分と2階微分の割合は-aとなることがわかります。

ここで、1.7933以下は割合から、2.05,1.88は、1.79から1.10について最小二乗法を用いることにより求めました。

この結果からも、aは一定値でないことがわかるため、仮定が怪しいことがわかります。

このグラフから類似した性質は、応力振幅と破断繰返し数ですね。