f(x)=-x^(n+1)+1+x+x^2+x^3+...+x^nの零点についての考察 その2 (問題提起)
- S Y
- 2023年2月6日
- 読了時間: 2分
0.参考文献
[1]
[2]
1.問題
次の零点を考えていました。

この零点を、対応する(n+1)についての関数としてどのようになるのか?を、前回の記事で検討し、失敗しました。(概算はできましたが…)
この(n+1)について、n>=0における整数全てを対象とした、関数f(x)の零点の性質を持つ、新しい関数F(x)を考えます。

この関数F(x)において、xの次数とそれに対応した係数は、どのような性質があるのでしょうか?これが、今回の問題です。
2.動機[2]
ある数論の問題で、素数pを法とした、yの3次式(左辺)とxの2次式(右辺)について、それぞれ左辺と右辺が等しいことを考えます。この解について、素数pと方程式の解の個数S(p)に対し、p-S(p)を考えます。これが、実はモジュラーな関数に対して、その次数と係数がp-S(p)と関係があることが実はわかります。
それと同様に、今回の式も、係数と次数が何かしらの関係性があるだろうと考えたのです。
3.関数f(x)の性質について
いきなり、別の関数h(x)を考えます。
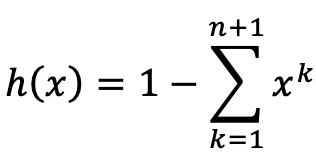
この関数の面白いことは、関数f(x)の零点からなる数列(すなわち、(n+1)ボナッチ数列) に対して、次の関係にあることがわかります。
例えば、フィボナッチ数列については、次のようになります。

同様に、(n+1)ボナッチ数列に対しても次の関係式があることがわかります。

h(x)とf(x)には、自明な次の関係式があります。
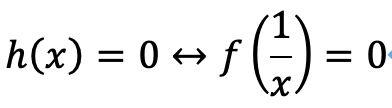
つまり、F(x)の零点を考えた時、この逆数は以下のH(x)の零点となることがわかります。

だから、F(x)の零点さえ考えたら、H(x)の零点も同時に求まるというわけです。
4.F(x)の部分積を展開する
実際にF(x)の部分積を考えます。
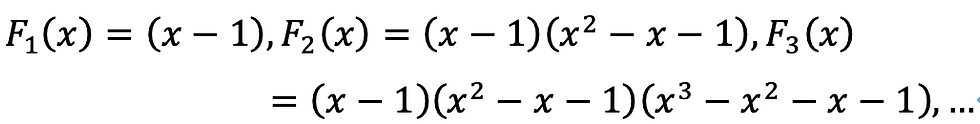
F(x)は、F_∞(x)となるわけです。
これらを実際に展開してみました。
x^0から、昇べき順に係数を並べます。

5.H(x)の部分積を展開する
実際にH(x)の部分積を考えます

実際に計算した結果、F(x)の部分積の昇べき順と、H(x)の部分積の降べき順の係数は一致することがわかりました。
6.(n+1)ボナッチ数列を係数にもつ多項式の零点について
次のようになります。

部分積を考えると、次のようになります。

実は、右辺と左辺を比較すれば、左辺は右辺のテイラー展開になっていることに気づきます。


コメント