足し算と掛け算を同値として扱うための方法
- S Y
- 2022年4月30日
- 読了時間: 3分
参考文献
1.0で割ってはいけない理由[1]
方程式を使った証明が一般的です。

a=b→a-b=0となります。4番目から5番目にかけて、仮に0で割れるとして計算を進めた結果、2=1という矛盾が発生します。つまり仮定が誤りであり、0では割れない。あるいは0で割ることは定義できないということがわかります。
方程式が苦手でなければ、この説明で十分納得いくかと思いますが、そうではない人にとっては難しいかもしれません。そこで、次の説明があります。
「0に対して何をかけても0になるので、1をかけようが2をかけようが同じになる。もし0を無視(割ってしまう)すれば、1と2は同じに見える。これは矛盾するので、0を無視して(割って)しまってはいけない。」
2.0と1しか存在しない世界
0と1しか存在しない世界での演算を考えます。特別な定義は次の式です。
1+1=0
要するに、2進数世界で繰り上がりなしという場合です。
以下の表はこの世界での、全ての足し算とその結果です。
↓(足す数) (足される数)→ | 0 | 1 |
0 | 0 | 1 |
1 | 1 | 0 |
同様に掛け算も考えます。
↓(かける数) (かけられる数)→ | 0 | 1 |
0 | 0 | 0 |
1 | 0 | 1 |
もし、0=1ならば、同値として見ることはできます。しかし、そうすると演算自体が不成立となります。
3.解空間による演算の対称性ついて
この解空間を2つの行列とみなします。

次に、この2つの行列に対し、足し算と掛け算の演算結果を考えます。
足し算は可換であり、結果は次のようになります。
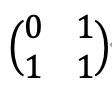
あるいは、転置行列が等しいことから、θ=π/2の“回転”変換と言っても良いかもしれません。
掛け算は非可換であり、結果は次のようになります。

ここで、この非可換性を修正するために、演算結果に何をかけたら可換性を見出せるかを考えました。そこで、何らかの回転操作を与えることで、可換性を与えられると考えました。

これを解くと、

となります。ここで条件として、|θ|=θですから、

よって、θがわかります。

仮に行列を2変数複素関数と見做した場合、その空間をつなぐ何らかの複素回転変換を考えることができます。(要するに、exp(iθ)による回転を行います。)
すると、次のような計算結果を得ます。

これを整理すると、次のようになります。

この近似値は、
±1.1102
です。
4. まとめ
足し算と掛け算の解空間を考えます。
→違いの解空間に対して、足し算は可換性があり、掛け算は非可換性があることがわかりました。
→無理矢理掛け算に可換性を持たせるよう、特別な回転変換を考えました。
→特別な回転変換では、特にθがただ2つに定まり、かつ絶対値は等しいことがわかりました。
→特別な回転変換をオイラーの公式に倣って回転空間での値を計算すると、値は実数になり、値はおよそ±1.1102であることがわかりました。
同様に足し算に対して特別な回転変換を考える時、θ=0、すなわち恒等変換を意味する行列となります。オイラーの公式に倣って計算すればそれは、1となることがわかりました。
この1.1102倍はどう考えたら良いでしょうか?
足し算の解空間と掛け算の解空間の相互演算解空間を考えます。相互演算解空間とは、足し算の解空間と掛け算の解空間をそれぞれ足した場合と、かけた場合の演算結果のことです。
計算した結果、足し算の場合は可換性が保存されているのに対して、掛け算は可換性が保存されないことがわかります。では可換性を保つために、どれだけ回転すれば良いのか、あるいはどの向きから見たら可換性が保存されて見えるかを考えます。
それが求めた回転角θです。それをオイラーの公式に倣って複素回転空間で考えると、exp(iθ)を与えることができるのです。
これが足し算の場合は1、掛け算の場合は1.1102倍となり、両者の演算の本質的な違いを、数値化することができました。


コメント