素数の間隔に対する予想

[1]予想の主張

以下の関係式が成り立ちます。そしていずれも同値です。

上の式：式1-1 真ん中の式：式1-2　下の式：式1-3

p<q<r: odd primes

つまり任意の素数は、自身より小さい素数の中で最大な2つの素数の和を上限として制限されるだろうことを主張します。

例を以下の表にまとめました。

図1-1

ちなみに、(p,q,r)=(3,5,7)の場合、式1-1は明らかに成立します。

[2]式1-1, 式1-3の二つが同値であることの証明(1)

次の式が同時に満たされると仮定します。

上：式2-1 下: 式2-2

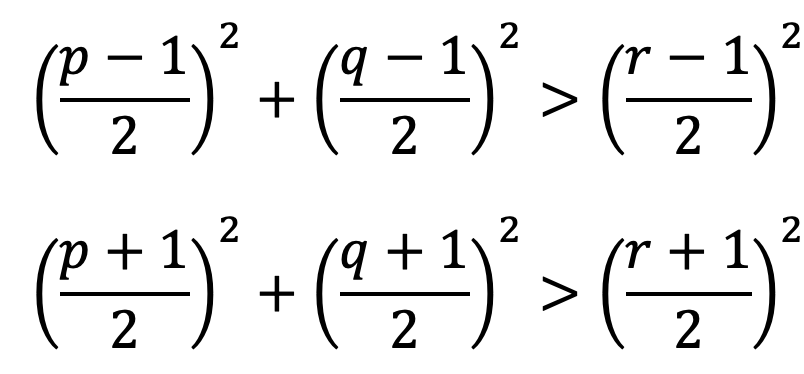
両辺を足して整理すれば、

式2-3

ここでp,q,rは全て奇数であるので、偶奇に気をつけると

式2-4

となります。

ここで、以下の補題を考えます。

さて、式2-1,式2-2について、ε_1,ε_2は、

ですから、条件を満たします。両辺をそれぞれ引くと、

このようになります。