特殊相対性理論をサイクル論で解く

1.特殊相対性理論とローレンツ変換

電磁気学で導かれたマクスウェル方程式によれば、電場と磁場をまとめて説明する方程式として、波動方程式が出てきました。それが、以下の式です。

ただし、tは時刻の、rは距離の次元を持っています。またこの波は等速で伝播する場合を考えています。

そもそも電場と磁場について捉えていたのに、この式には一見その2つが見えません。どこに行ったかというと、定数cなのです。つまり、電磁波の性質はまとめて定数cにされたのでした。

ところで、このc^2は真空の誘電率と透磁率の積の逆数になっていることがわかります。

(詳しくは、電磁気学で学べます。)そこで、cは真空を伝播するとき、いつでも同じ値を取ることがわかります。

ここに、真空中を伝播する、常に一定の波が存在することがわかりました。そしてそれこそが光であることに、その速度と当時知られていた光速が一致することから気づいたというわけです。

ところで、速度についてガリレイ変換によればベクトル合成が可能であることがニュートン力学で知られていました。簡単に説明すると、動く歩道を転がる球の速度は、動く歩道に乗っている人と乗っていない人とで、動く歩道の速度分、異なるというものです。

ところが、光速という概念は、このガリレイ変換が成り立たない(つまり、観測者に依存しない絶対量である)ことがわかったのです。

そこで、等速直線運動している物体が、静止していた時に比べてどのくらい距離および時間が「変形」したのか？を考えるために、ローレンツ変換というものが出来ました。それが以下の式です。

ここに、βおよびγは以下の通りです。

βは、実際はエントロピーとは異なる次元を持つ無次元量ですが、「ある系の許される最大速度に対する速度の比率」と捉えることで、「ある系の乱雑さ」を示していると考えられると思います。乱雑さはまさに、エントロピーのことですから、確かに正しそうです。

2.サイクル論との相似性

ローレンツ変換で登場する行列は次のように整理することができます。

ただし、次のように定義しました。

よって、ローレンツ変換で使われる場は、ある種の温度行列であることがわかりました。すなわち、次のように示せます。

同様にして、次の結果を得ます。

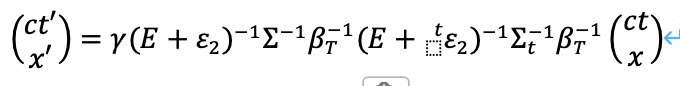
2つの温度行列について、以下の関係にあることがわかります。

すなわち、次のようになります。

やはり、サイクルが存在することがわかりました。

言い換えると、特殊相対性理論は、サイクル論の特別な形であることがわかりました。

最新記事