無数に素数を与える円分多項式が、無数に存在することの予想とその主張・懸念事項など

0.参考文献

Hatena Blog INTEGERS 分野コフスキー予想と41と1091

高校数学の美しい物語　フェルマーの小定理の証明と例題

1.ブニャコフスキー予想[1]

定数でない整数係数多項式に対して、f(n)が素数となるnが無限に存在するための必要十分条件は次の3条件を満たすことであろう。

1 f(x)の先頭係数が正

2 f(x)は整数係数多項式として既約

3 nが正の整数全体を動く時、全てのf(n)を割り切るような1より大きい整数は存在しない。

詳しくは、参考文献[1]に書かれてあります。

2.フェルマーの小定理[2]

pが素数で、aがpの倍数でない正の整数の時

(式2.1)が成り立ちます。詳しくは、参考文献[2]に書かれてあります。

3. p番目の円分多項式とは

ものすごく雑に説明すれば、公比x、初項1、(p-1)番目までの幾何級数のことです。

4. フェルマーの小定理から、円分多項式を導く

式2.1について、ある自然数kを用いて次のように書き換えられます。

(式4.1)左辺は明らかにxで割れるので、これは合成数となります。

ここで、p, x, b, b+1が全て互いに素となるbを与えましょう。式4.1の両辺にそれぞれbを加えます。

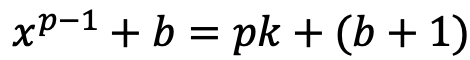
(式4.2)右辺をみれば、ディリクレの算術級数定理が使えることに気づきます。すなわち、右辺の形をした素数は無限に存在するのです！

ここで左辺に注目すると、円分多項式となっています。つまり、このような形の円分多項式は無数に存在することがわかります。

ここで、同様にしてb, b+1と互いに素となるような素数q, cを考えます。この時、式(4.2)に倣って作成した

(式4.3)について、式4.2と合成した以下の形の方程式

(式4.4)も、無数に素数が現れるでしょう。

5. ブニャコフスキー予想に対する考察

1は、先程の合成(式4.4)を考えた時に、先頭係数が正でなければ右辺の1次多項式の結果が負になってしまうため、その観点から必要十分条件となります。

2 は、右辺が既約であることから、f(x)も既約となるし、反対にf(x)が既約でないと仮定すれば、因数分解できるので結果が素数となることはありえない。背理法からf(x)は既約であるとわかります。その観点から必要十分条件となります。

3 右辺を見れば、全ての係数は互いに素となりますので、nがどのように動こうとも、それら全てを割り切るような整数は1以外にありません。ですから、十分条件となるでしょう。

6. 反論(by 戸松村)

式4.2に対して、kは任意にとることはできません。左辺のp,bに対応した値をとります。その場合、pk+(b+1)がとりうる無数の非素数と対応し、ディリクレの算術級数定理は適応できない可能性があります。

最新記事