接続球から分離球への変換、分離球から接続球への変換を、実数階微分により説明する
- S Y
- 2022年12月25日
- 読了時間: 1分
0.参考文献
[1]
1.分数階積分学[1]
積分の階数は、高校数学では自然数階で定義されていました。また、これを負の整数に拡張すれば、それは正の整数階、微分することでした。
実は、負の整数を除く複素数αについて、α階積分は、次のように与えることができます。

2.cosh(φ)とsinh(φ)の実数階積分
特に、cosh(φ)とsinh(φ)について、φで積分することを考えます。この2つは、負の整数階積分することと、自然数階積分することは一致するのが特徴です。cosh(φ)をz階積分する時、zの絶対値が奇数だとsinh(φ)に、zの絶対値が偶数だとcosh(φ)になります。
そのため、分数階積分で定義したαについて、負の整数を含めても、cosh(φ)とsinh(φ)に対しては成立することがわかります。つまり、複素数αによるα階積分を考えられるということになります。
3.接続球から分離球への連続的変形を、分数階積分で説明する。
接続球について、方程式やパラメータは次のとおりになります。
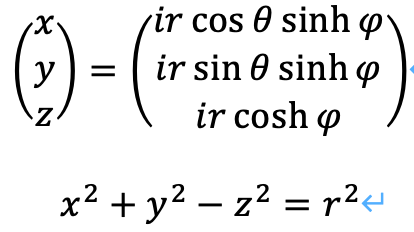
分離球について、方程式やパラメータは次のとおりになります。
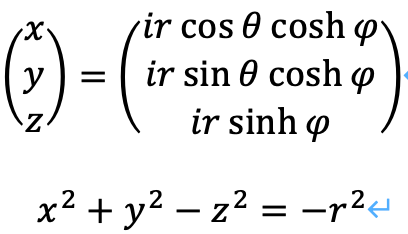
接続球から分離球までの変形時間[0,t_end]を無次元化して、[0,1]とします。この無次元時刻αを考えると、パラメータは次のように表せます。

このパラメータを用いることで、無次元実数時間αの変化を説明することができました。


コメント