完全直方体が存在しないことの証明
- S Y
- 2021年8月2日
- 読了時間: 3分
0. 参考文献
きょうの数字:「44」
Euler brick - Wikipedia
ピタゴラス数連続発生式
ピタゴラス数を作り出す公式
1. オイラーのレンガ
全ての面の辺と対角線の長さがいずれも自然数となる直方体は、「オイラーのレンガ」と呼ばれます。例えば最小の3辺として、"44, 117, 240"が挙げられます。実際、以下の計算式が成り立つことからわかります。[1]

これには特に、パラメータ表示の存在が知られています。参考文献[2]に詳細が説明されてあります。
2. 未解決問題
完全直方体とは、全ての面の辺と対角線の長さに加えて、直方体の対角線も自然数となる直方体のことを言います。存在するか否かという問題が未解決です。
つまり、各辺(a,b,c)と各面の対角線(d,e,f)に加えて、直方体の対角線gも自然数であるということになります。なお、それぞれの文字の関係は以下の通りになります。

3. ピタゴラス数連続発生式と、原始ピタゴラス数生成式
以前研究所のメンバーである戸松村が発見した、ピタゴラス数連続発生式[3]を復習しておきましょう。

もう一つ、原始ピタゴラス数生成式[4]というものが知られています。まとめると以下のように説明できます。

4. 完全直方体が原始ピタゴラス数によって作られないことの証明
原始ピタゴラス数が、

で与えられたとしましょう。この時、自然数m,n(m>n)が存在して、

となるとします。
さらに、αが対角線となるような原始ピタゴラス数の組み合わせ

とαの3つひと組があり、以下の式を成り立たせると仮定します。
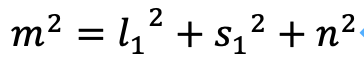
同様の方法を繰り返すことで、以下の式が生成されていきます。

すなわち、あるα_nに対して、次の方程式がなり立ちます。

ここで、直方体の面について、対角線、短辺、長辺が全て自然数となるように、それぞれの長さが原始ピタゴラス数(l_n, s_n, s_(n-1))と等しいとしましょう。代入すれば、以下の関係式が成り立ちます。

両辺は0より大きいので、

これは、l_(n-1)とl_nがいずれも自然数であることに反します。(仮にいずれも自然数であれば、2の平方根が無理数でないことになり矛盾する。)
以上の方法では、完全直方体を探せないことがわかりました。
一方、βが対角線となるような原始ピタゴラス数の組みが存在するとしましょう。この時、自然数

が存在して、

を成り立たせます。
ところで、ピタゴラス数連続発生式[3]より、l_1, s_1とαはβを通して以下の関係式を成り立たせます。

一方、γとαについても以下の関係があります。

以上から、γを通して、l_1, s_1とm,nは以下の関係にあることがわかります。

この式を少し変形していきましょう。

仮に右辺が

であるとすれば、以下のように変形できます。ここで平方完成ができるように、mn=l_1としました。

ところが、

であるから、l_1=s_1=1となります。この結果から、自然数m,nの値もわかり、m=n=1であることがわかります。
l_1=s_1=1の結果からわかることは、βを対角線とする三角形のある一片が0となることです。(結果1)
また、m=n=1の結果からわかることは、αが0であることです。(結果2)
ちなみに、結果2が成り立つ時、結果1も成り立ちます。
以上の方法では、三角形を作れないことがわかりました。
以上から、原始ピタゴラス数を使って完全直方体を作成することは不可能であることがわかりました。
5. 完全直方体が一般に存在しないことの証明
一般のピタゴラス数を使って完全直方体を作成しようとします。ところが一般のピタゴラス数によって作成された三角形は、原始ピタゴラス数によって作成されたものの相似形であるため、4章で考察したことと同値の結果を得られます。
重ねて申し上げますが、ピタゴラス数を使わないで完全直方体を作成しようとすれば、対角線が無理数となりますので、できません。
以上から、いかなる数の組み合わせでも、完全直方体を作成することは不可能です。
6. 結論
4章から、原始ピタゴラス数から完全直方体を作成できないことがわかりました。5章では、一般のピタゴラス数や他の数からも完全直方体を作成できないことを確認し、完全直方体は存在しないことがわかりました。


コメント