双対数についての式(その2)

参考文献

[1] https://ja.wikipedia.org/wiki/ランベルトのW関数　

式1

導出

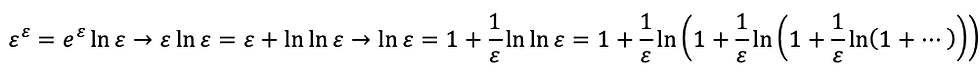
式2

導出

同様にして、

式3

式2の結果や、ζ(0)の導出方法をそのまま使うことにより明らかです。

この結果から、次がわかります。

式4

この式は、計算値では間違っているし、全部計算すると発散しますが、次のグラフのようになります。

横軸: k、縦軸:k番目までの素数で求めたεの計算値

軸の切片はやはり興味を持ちます。"0番目の素数"までの時、εの計算値は-0.45程度になるようです。また、εの計算値が0に限りなく近づくのは、"-0.7番目位の素数"まで計算した時となります。

(0.45/0.7~0.64~0.66は偶然でしょうかね？)

式5

Gは、万有引力定数。力や質量が正規化された場合、1/4πになるのでは？

ただの予想です。電磁気に関するクーロン力の係数に真空の誘電率、透磁率が関わっていることから、もし重力に極が存在したとした場合(反重力が立証された場合)、真空の重力伝達率γ_0が定義されるべきです。しかも、実はそれがどのような値をとってもよいということを二元数から推測することができます。ちなみに、ビオ・サバールの法則の際、経路積分を用いた結果、分子に出てくることから、これを基準にしました。(定義によっては、1/(4πε_0^(j^2))でも可)。

式6

これは、次の一般化した方程式の解が関係します。

この解は、一般に次のように与えられます。[1]

さらにこれを原点を中心にテイラー展開すると、次のように一意に与えられます。(収束半径は1/e)

よって、z=-exp(±ε+lnε)を代入すれば、-W(z)=εとなります。

以上から、x=±ε-lnεが導出できます。