双対数εのローラン展開に関する考察

0.参考文献

[1]https://ja.wikipedia.org/wiki/二元数　

[2]https://ja.wikipedia.org/wiki/分解型複素数

[3]https://ja.wikipedia.org/wiki/オイラーの公式

[4]https://isiotoyume.wixsite.com/website/post/双対数εについての関係式

[5]https://laid-back-scientist.com/taylor-series2

[6]https://ja.wikipedia.org/wiki/テイラー展開

[7]https://manabitimes.jp/math/787

[8]https://www.chugenkon.org/public/great/125.html

1.cosμ(εx)、sinμ(εx)

1.1 二元数[1][2][3][4]

ここでは、二元数ついて説明します。二元数は3つ存在します。

また、iとjに対しては以下の式が成り立ちます。

1.2復習

先の2つに倣い、双対数εに対しても類似した式を考えます。

まず、前回紹介した関係式があります。

これについて、左辺をexp(εx)とした場合、次のようになります。

両者はεがうまく微分を与えること、あるいはテイラー展開によって容易に証明可能です。

1.3cosμ(εx)、sinμ(εx)[5]

次の関係式を成り立たせるとします。

これを成立させるようなcosμ、sinμをうまく定義しようと思います。余談ですが、μを使っている理由は、hを水平線線対称した形とμが似ているので、そういうデザインにしました。

まずは、cos、sin、cosh、sinhのテイラー展開を考えます。

これに類似した形で、以下のように定義します。するとこの級数は収束します。

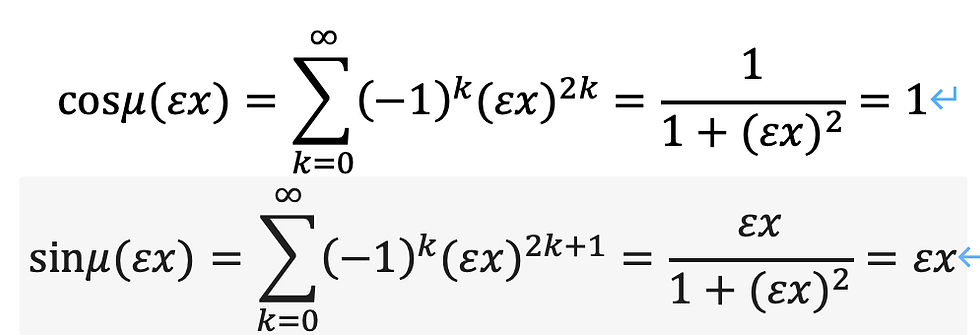
こうして、うまく定義することができました。

2.テイラー展開[6]

2.1方法A

2.1.1微分の無限化

θ=εxとして、θで微分することを考えるとき、本来ならcosμ(εx)、sinμ(εx)はそれぞれ1回微分、2回微分で定数(=0)となります。

しかし、あえて次のように考えることで、これを解消します。

2.1.2定理

微分が積分の逆であることに注意し、不定定数をうまく0にすれば、以下の式が成り立ちます。

ただし、[ε]^mは双対数からなるm次空間とします。(2次以上の空間だと本来0になるため、1-(-2)=3の逆数となると考えられるように思います。)

2.1.3テイラー展開

テイラー展開は次のように定義されます。

xがaに対して十分近づいたとき、この等式は成り立ちます。(高次の項の影響が少なくなります)。

これを用いてexp(εx)をテイラー展開します。

2.1.4考察

exp(εx)=εx+1ですから、最右辺と比較すれば、次の等式を得ます。

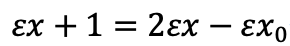
ここで、双対数が微分を与えることに注意すれば、次の関係式を得ます。

一方、微分の定義式は次のとおりです。

すなわち、次の関係式を得ます。

これを右辺に代入します。

よって、次の式を得ます。

以上から、0=1となりました。この結果は、0で割ってはならないことを説明するものでした。また、これをうまく説明するために、超弦理論を導入しました。

2.2方法B[7][8]

cosμ(εx)、sinμ(εx)の定義式を見ると、arctangentの微分に似ていることに気づきます。

以上から、θ=εxに対して、次のように書き換えることができます。

ここで、arctangentについてマクローリン展開を与えます。

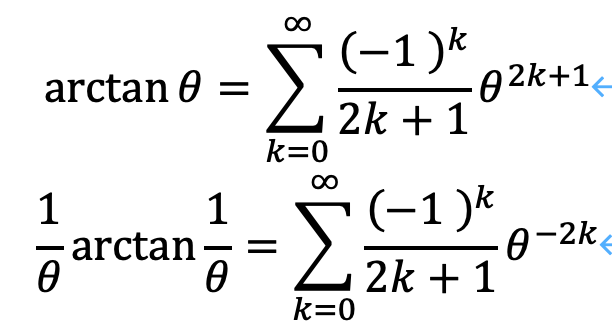
(上：正しい　下：本当は正しくない)

ただし、前者は|θ|<1、後者は|θ|>=1が条件となります。ここで、θ=εxですから、距離の定義より|θ|=0となります。よって前者が正しいことがわかります。

さて、一度θ=εxを代入してみましょう。すると、次のようにローラン展開できます。

ここで、1.2の式から、次の関係式が成り立ちます。

よって、両辺にεxをかけ、次のように整理することができます。

特にx=1の時は次のようになります。

また、x=iが可能であるとしたら、次のようになります。

よって、両辺をi倍すれば、

x=1の場合の両辺を足すことにより、次の結果を得ます。

また、同様に両辺を引くことにより、次の結果を得ます。

x=εの場合を考えます。

これは、異なる次数の無限大が、有理数倍されることにより互いに等式で結ばれることを意味します。これを整理すれば、異なる次数の無限大についての無限多項式が、有理数(有限値)に置き換えても良いことになります。

これに類似した話で、朝永振一郎先生のくりこみ理論(電子の質量と電荷を、理論値の∞に対して実験値の有限値に置き換えることで、他の電子に関する現象を、それまで知られていた理論で説明できるとする主張のこと)があります。おそらく、無限大に関する様々な計算結果が、有限値に置き換わることと、今回の結果は何らかの関係性がありそうですね。

一般化すれば、次のようになります。