双対数εについての関係式
- S Y
- 2022年2月11日
- 読了時間: 3分
0.参考文献
1.双対数とは?[1]
定義

実際、複素数の範囲で解を求めることは出来ません。

この方程式の面白いところは、自動微分してくれるところです。以下のようなテイラー展開された関数f(x)について、容易にその微分を与えます。


εの係数が、f(x)の微分値となっていることがわかります。
テイラー展開は関数f(x)がC∞級であることだけが条件であったので、この等式もC∞級の関数であれば成立します。
さらに、CN級の関数に対しても同様に微分値を与えます。
2.定理1
以下の等式が成立する関数f(x)は唯一定まり、f(x)=exp(x)となります。

ここで、双対数を用いて表します。

以上から、次の定理が成り立ちます。
定理1

両辺をm(自然数)乗すれば、以下の関係式を得ます。
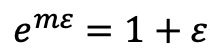
逆数を考えると、次のようになります。
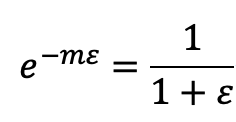
3.定理2
オイラーの等式は以下の通りです。[2]

また先ほど得た等式を整理すれば以下のようになります。

両辺を足すと、以下のようになります。
定理2

4.定理3
定理1を変形すれば、以下の等式を得ます。

定理2に代入して整理すると、以下のようになります。
定理3

5.定理4
定理3の形から、第二項までがexp(iπ)になっていることに気づきます。

exp(iπ)に対して全て-1を代入することで、次の式を得られます。

さて、この章の目標として、以下のkについて考察することとします。

εについての式を先ほどの式に代入し、整理することで次の結果を得られます。

両辺の対数を取ります。

kについて解きますと、次のようになります。また、kの定義式から、定理4を得ます。

定理4

この形は、次の微分公式に似ています。

6.定理5
定理4について、両辺をexp(ε)でわり、さらにexp(左辺)=exp(右辺)の関係式を用いると、以下の関係式を得ます。
定理5

7.定理6
定理5の両辺を2乗することで、定義から以下の関係式を得ます。
定理6
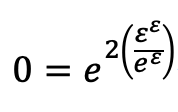
8.定理7
定理5の対数を取れば、定理7を得ます。
定理7

9.定理8
今回は実数、虚数、双対数の関係式を考えます。
以下の関係式が成り立つことは容易にわかります。

3つ目までの両辺をそれぞれかけることで以下の式を得ます。
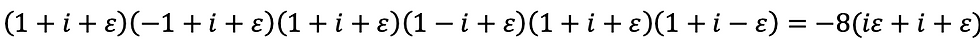
4つ目の式を代入して整理することで定理8を得ます。
定理8

両辺にiをかけて整理すれば、次のように変形することもできます。

10.定理9
容易に以下の等式が成り立つことがわかります。
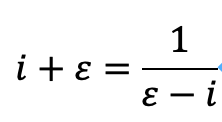
11.定理10
次に、Γ関数に代入してみます。今後、もしかしたらリーマンのζ関数に対して使えるかもしれない定理です。
定理10 (nを0以上の整数とします。)

ただし、γ関数が双対数でも複素数の際と同様に定義できるものとし、かつ双対数と実数のなる空間で全微分可能であると仮定した上でのものです。
12. 定理11
次の等式を考えます。
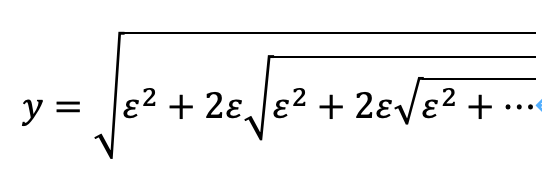
両辺を2乗して整理すると、

解の公式を用いて、yについて解きます。

また、ε^2=0ですから、以下の関係式が成り立ちます。
定理11

すなわち、

13.定理12
定理1から、以下の関係式を導出できます。

第2辺と最右辺に対して対数をとると、次のようになります。

本来、双対数に対して逆数を定義することは出来ませんが、不思議なことに以上の方法で逆数のようなものを与えることが出来ました。


コメント