一般化モンティ・ホール問題
- S Y
- 2023年2月20日
- 読了時間: 2分
0.参考文献
[1]
[2]
1.モンティホール問題[1]
扉が3つあります。1つは正解で賞品が、残り2つは不正解で何も入ってません。出題者はどこに正解があるのかを把握してます。この時、挑戦者はあらかじめ一つ選択をし、出題者は残りの2つのうち一つ、不正解であるものを除きます。
この時、挑戦者は残った2つのうちどちらを選んだ方が良いのか、選択を変更した方が良いか、しない方が良いのか?を考えます。
この問題の答えは、「選択を変更した方が良い」となります。確率が2倍変わるためです。
仮に、扉の色を青、黄、赤とします。青を最初に選択した場合、「挑戦者が黄色を除いて、赤色に変更する」、「挑戦者が赤色を除いて、黄色に変更する」と、「いずれにせよ青色を選択する」の3通りとなります。変更する場合は、当たる確率が赤色と黄色の2/3、変更しない場合は、当たる確率が青色の1/3となります。以上から、変更した方が確率が2倍となることがわかります。
2.一般化モンティ・ホール問題
扉の数を任意の自然数nにします。また、出題者は挑戦者が選ぶごとに、一つ不正解の選択肢を外すこととします。
この時、挑戦者が選択肢を変更した時に当たる確率p1を求めます。

この時、さらに出題者が不正解の選択肢を外すこととします。
この時、挑戦者が選択肢を変更した時に当たる確率p2を求めます。
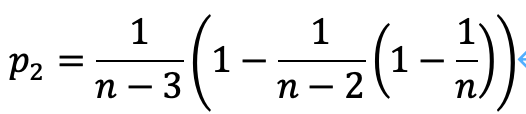
以上を一般化して、m(<n)回目の時、次のようになります。

3.n=-1の時[2]
モンティ・ホール問題は、扉の数が自然数ある必要があります。これを一般化すれば、確率について式を与えることができます。
ここで、n=-1を特に考えることとしました。これを式に代入して整理すれば、次のようになります。
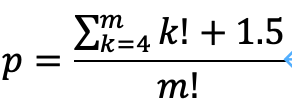
ここで、ポッホハマー記号[2]を用いることにより、次のように整理することができます。

ちなみに、p-1の分子はよく、素数になることがあります。


コメント