ルジャンドル予想に対する感想

0. 参考文献

[1] https://youtu.be/YNmRhCNvBbg ルジャンドル予想　予備校のノリで学ぶ「大学数学・物理」

[2] https://www.chart.co.jp/subject/sugaku/suken_tsushin/91/91-4.pdf　ベルトラン・チェビシェフの定理を使う　〜n!(n>=2)は平方数ではないことの証明〜

1 ルジャンドル予想とは？

任意の自然数nに対し、n^2と(n+1)^2の間には必ず素数があるだろうという予想のことです。[1]

2 ベルトラン・チェビシェフの定理

nと2nの間には、素数が少なくとも1つ存在するという定理です。[2]

3 ピタゴラス数連続発生式の復習

ピタゴラス数連続発生式は、戸松村によると以下の通りです。(式1)

ここで、仲間はずれがa^2であることに気づきます。(他の二つは、次元がa^4だから。)わかりやすいように、右辺とa^2をそれぞれ移行し、a^2をnと置き換えてみました。(式2)

また、以下の式が成り立ちます。(式3,4,5)

4 n^1クラスとn^2クラスの関係性

これはあくまで感覚的なものです。ちゃんとした数学ではないのでご容赦ください。

初めに、n^1クラスの数直線と、n^2クラスの数直線をそれぞれ別々にイメージします。n^1クラスは等間隔に1,2,3,...n,n+1,n+2,...と並んでいます。一方、n^2クラスの数直線は、nが大きくなるにつれて間隔も大きくなっていきます。

さて、それぞれの数直線に対し、nとn^2で結んでみます。

すると、数直線と結んだ線でベクトル演算が可能になります。うまく数直線を配置することで、直角三角形も作れます。

平行な2直線：n^2クラス。視点座標の変換により、ある無限遠で交点をもつ

垂線：n^1クラス

平面から見た場合の図。平行線は交わらない。

視点を変えた場合。ある決まった無限遠が各nに対して一意に存在する。無限遠での交点は、例えば絵画の1点透視図法などで見られる。

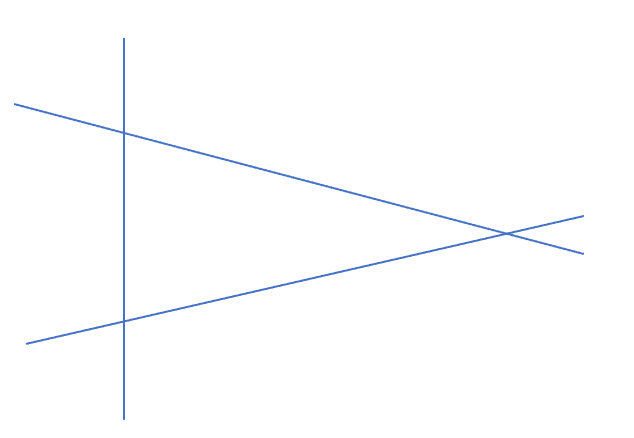
ピタゴラス数連続発生式なので、4nと(n+1)^2, (n-1)^2からなる三角形は、各nに対応するような、直角三角形となります。ですから、数直線をうまく配置させることで直角三角形を作ることは、well-definedだと思われます。

なんとなく、n^2クラスの性質と、ピタゴラス数連続発生式によって変換されたn^1クラスの性質は同じであるのではと感じられます。

ここで、ベルトラン・チェビシェフの定理から、nから4nまでの間には、少なくとも2つ以上の素数が存在することがわかります。nから2nで少なくとも1つ、2nから4nまでで少なくとも1つ。合計で少なくとも2つ以上となります。

また、中間地点の2nについて、2nは明らかに素数でないので、nから2n-1, 2n+1から4nと分けて考えることもできます。

この結果からわかることは、先程の式3,式4の左辺について、n^2-(n-1)^2というベクトルに等しい、n→2n-1の中に素数が1つあることを、(n+1)^2-n^2というベクトルに等しい、2n+1→4nの中に素数が1つあることを、それぞれ意味しているだろうことです。

これは、ルジャンドル予想が正しいことを説明しています。

5 「証明」と言わなかったことについて

Well-definedだろうと思われますが、その具体的な証明がわかりませんでした。ですから、あくまで感想止まりとしてここに記載しておきました。また、n^2クラスの性質と、n^1クラスの性質が実際に同じであるのかについての証明もわかりませんでした。