リーマンゼータの零点を満たすs=1/2+ibについて、bが満たす条件

文献

[1]https://ja.wikipedia.org/wiki/リーマンゼータ関数

1.リーマンの関数等式[1]

リーマンによれば、ゼータ関数は以下の等式が成り立ちます。

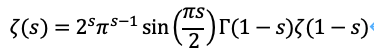
2.ζ関数の入力値sを実部と虚部で分けることは可能でしょうか

この式が成り立つと仮定し、その補正項Xを求めたい。s=a+ibとします。

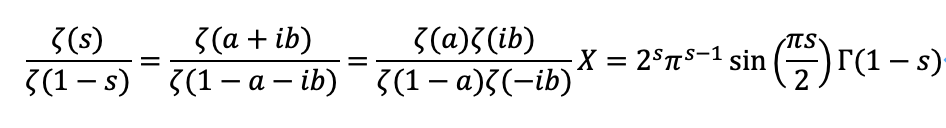
2.1 T(s)=2^sについて

積により分けられました。

2.2 P(1-s)=π^(1-s)について

補正高はπ^(-1)である。それを認めていれば、積により分けられました。

2.3 Γ(1-s)について

まず、ガンマ関数もどきを定義します

このように定義したとき、元のΓ関数とは以下の関係にあります。

これをもとに、Γ(1-s)を考えます。

補正項2^(-1+a), 2^(-1+ib)を与えることで、積により分けることができました。

2.4 sin(s)について

明らかに、sin(a+ib)≠sin(a)sin(ib)である。そこで、補正項sin(a+ib)/{sin(a)sin(ib)}を求めます。

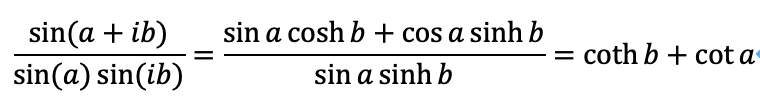
2.5 全体の補正項Xについて

これを整理して、

ここで、

であるから、a=1/2を代入したとき、X=1となることがわかります。

この時、bについての式は以下のようになります。

2.6 結論

以下の条件を満たします。