フィボナッチ数とそのフィボナッチ数以上、かつ最も近い素数との差の関係についての予想

1 予想

任意のフィボナッチ数に対して、そのフィボナッチ数以上、かつもっとも近い素数との差を、ゼッケンドルフ表現で表します。このゼッケンドルフ表現で現れるフィボナッチ数の最大値について、それがm番目、元のフィボナッチ数がn番目であるとすれば、mとnには以下の関係式が成り立つでしょう。

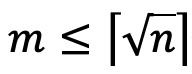
2 例

1~5: それ自身

8(5番目): 11. 11-8=3(3番目).

13: それ自身

21(7番目): 23. 23-21=2(2番目).

34(8番目): 37. 37-34=3(3番目).

55(9番目): 59. 59-55=4=3(3番目)+1

89: それ自身

144(11番目): 149. 149-144=5(4番目)

233: それ自身

377(13番目): 379. 379-377=2(2番目).

3 考察

形が似ている(1/2乗か、2乗か)ので、ルジャンドル予想と関わりがありそうですね。